Reinhard Fössmeier
Per la esprimo "novaj komunikiloj" oni nomas elektronikajn komunikilojn kiaj telekopio, video-teksto, ekran-teksto, elektronika posxto. Tiuj komunikiloj komencis sxangxi niajn komunikajn kutimojn. Kiuj estas la karakterizaj ecoj de tiu "nova komunikado"?
Skriba komunikado. En la historio de la homa komunikado elstaras tri inventajxoj, kiuj sxangxis la komunikajn kutimojn. La unua tia inventajxo estas la skribo, kiu venkis la limojn de spaco kaj tempo: Kion iu homo skribis ie kaj iam, alia povas legi en ajna distanco kaj je ajna tempo, ecx longe post la morto de la skribinto. Tiel komunikajxo povas atingi ne nur cxeestanton, ne nur grupon en vok-distanco, ne nur samtempulojn, sed ajnan nombron da homoj.
Elektra komunikado. La dua inventajxo, kiu forte influis la komunikadon, estis la elektra inform-sendo, per telegrafo kaj telefono, kaj poste per elektromagnetaj ondoj, do radio. Gxi venkis la limojn de rapideco, tiel ke komunikajxo nun povas disvastigxi per la rapideco de la lumo anstataux tiu de marsxanta homo, de cxevalo aux kolombo. Tiun limon jam antauxe atakis la komunikado per lum- aux fum-signaloj, sed ilia apliko estis komplika kaj necerta.
Diskretigita komunikado. La tria inventajxo tempe miksigxas kun la unuaj du, fakte ecx ebligis la unuajn pasxojn de la dua: temas pri la diskretigo de analoga informo. Jam la transiro de desegnajxoj al (ideograma aux alfabeta) skribo signifas tradukon de informo en aron de klare distingeblaj informeroj, kies inform-enhavo do estas klare fiksita. Ecx pli klara estis tiu pasxo cxe la unua apliko de elektra komunikado: longe antaux la invento de la telefono oni povis transsendi tekstan informon per la morso-kodo. Nur poste la elektra komunikado povis reveni al la komunikado de vocxaj informoj.
Auxtentikeco. La transiro de vocxa al skriba inform-intersxangxo malfaciligis la kontrolon de la auxtentikeco: estas multe pli facile falsi leteron ol personan komunikadon, kiu inter konatoj estas preskaux ne falsebla. Tiun mankon de la skribo oni kompensas per signaturo (subskribo), stampoj, specialaj paper-specoj kaj pres-teknikoj (plej konate cxe bank-biletoj). Aliflanke la auxtentikeco de skriba komunikajxo estas kontrolebla je ajna tempo, ankaux post gxia estigxo. (laux PIV [17] estas eta diferenco inter subskribo kaj signaturo: subskribo atestas la auxtorecon, signaturo la verecon de dokumento. Cxar ni okupigxos pri la unua, mi cxefe parolos pri subskriboj, kvankam laux [17] subskribo cxiam konsistas el la nomo de la subskribinto, kio ne estas vera pri la diskutotaj metodoj.)
El la elektraj komunikiloj, la telefono posedas certan auxtentikigan povon; telekso donas almenaux iun sekurecon pri la sendanta stacio. Cxe telegramoj, la reguloj almenaux malpermesas erarigan subskribon, sed la kontrolo estas malfacila. Entute la elektraj komunikiloj malbone subtenas la auxtentikigon.
La esprimo "nova komunikado" signifas esence la grand-skalan aplikon de elektra (elektronika) kaj diskretigita (digxita) komunikado: la uzataj sistemoj estas telekso, telekopio, video-teksto kaj la "elektronika posxto", cxi-lasta ekzemple kadre de la t. n. ekran-tekstaj sistemoj. Komunaj al tiuj sistemoj estas la ne-ligiteco de la informo al materia portajxo aux substrato (kia papero) kaj la klara difiniteco de la inform-enhavo: Mankas iaj krom-informoj, kiuj povus servi por auxtentikec-kontrolo (auxtentikigo). Tiu problemo estas longe konata en telegrafio kaj kondukis al la praktiko, ke en komercado cxiu telegrama komuniko devas plejeble rapide igxi konfirmita per letero.
Kial la telegrafion, kiu estas elektra kaj digxita, oni kutime ne envicigas inter la novajn komunikilojn? Ne precipe pro gxia malnoveco, sed pro la fakto, ke la tradicia vojo de telegrama mesagxo ampleksas ne nur la elektran parton, sed ankaux la akcepton kaj liveradon fare de homaj dungitoj. Tiuj partoj, kiuj ne estas digxitaj, diluas la digxitecon de la telegrafio, kaj certagrade ebligas auxtentikigon.
Unuaj solvoj. Unuavide povus sxajni, ke telekopiado solvis tiun problemon, cxar tie literoj estas reprezentataj ne per iu kodo, sed per sia formo, konsistanta el nigraj kaj blankaj punktetoj. Sed tiu punkt-informo estas same facile kaj nekontroleble kopiebla kaj miksebla kiel la kodoj de telekso.
Parte oni solvas la problemon per transakciaj numeroj (TAN) kiujn la korespondantoj antauxe intersxangxas laux absolute sekura vojo, kaj poste uzas por auxtentikigi siajn mesagxojn: Cxiun mesagxon devas akompani nova TAN, en la gxusta sinsekvo. Ekzemple bankoj provizas siajn klientojn per TAN-oj, indikendaj cxe cxiu komisio al la banko. La metodo de TAN-oj postulas senprokrastan komunikilon, kia telefono, cxar se iu falsisto povus kapti kaj iomete prokrasti mesagxon, li povus intertempe mem uzi ties TAN-on. Pro tio kaj pro la malkomforteco TAN-oj ne estas perfekta solvo.
La matematiko nun disponas pri metodoj, kiuj ebligas komfortan digxitan komunikadon kun auxtentikigo. Tiuj metodoj estos la temo de cxi tiu kurso.
En cxi tiu kurso ni parolos pri kodoj kaj cxifroj.
Ambaux nocioj estas bone difinitaj en la Plena Ilustrita Vortaro [17].
Ne ekzistas tie vortoj 1e) por la scienca brancxo, kiu traktas la cxifradon,
kaj 2e) por la tekniko de gxia apliko.
Iván en [10] por la unua proponas la
terminon kriptologio,
uzatan en pluraj lingvoj.
En [12] estas menciata la vorto kriptografio,
kun senco ne tute klara inter 1 kaj 2;
cxar vortoj kiaj
telegrafio kaj fotografio havas,
same kiel parencaj vortoj en aliaj lingvoj,
pli praktikan signifon;
mi uzos la vorton kriptografio ankaux en la internacia lingvo
por nomi la teknikon kaj aplikadon de cxifrado.
2 Kodoj kaj cxifroj
La nocioj "kodo" kaj "cxifro" foje estas konfuzataj, cxar la unua enhavas la duan. El la bonaj difinoj en [17] por ni utilas jenaj partoj:
Resume ni povas diri, ke cxifro estas sekreta kodo, aux pli precize, ke gxi estas kodo uzata kun la intenco kasxi informon kontraux iu.
Kodo estas funkcio, kiu bildigas signaron (vort-aron) al alia signaro (vort-aro).
Konataj ekzemploj estas:
|
a) rekono per duobligo de la informo (tre kosta):
akademio + akademio : en ordo akademio + ikademio : eraro! | ||||||||||||
|
b) korekto per triobligo de la informo (ecx pli kosta): akademio + akademio + akademio : en ordo akademio + ikademio + akademio : akademio kredeble estas gxusta! | ||||||||||||
|
c) rekono per kontrol-cifero;
la sumo de cxiuj ciferoj estu dividebla per 10:
|
La celo de kodo estas tauxgeco por komunikado laux diversaj vidpunktoj: La komunikado ne estu tro kosta, kaj la originala informo estu rekonstruebla, eble ecx sub malfacilaj cirkonstancoj kia perturbata kanalo, kaj per lauxeble simplaj rimedoj. El tiu celo sekvas diversaj kriterioj por la kvalito de kodoj:
Ekzemplo por koncizeco estas la morso-kodo, kiu utiligas la plej mallongan kodon (.) por la tre ofta litero e. Ekzemplo por sekurigo de kodo estas la aldono de kontrol-cifero, kiu kompletigas la sumon de la koderoj al iu fiksita valoro; se post la transsendo tiu sumo estas malgxusta, nepre okazis eraro (v. figuron 1c).
Inter tiuj kriterioj gxenerale necesas kompromisoj. Kompreneble la deziro je koncizeco kontrauxas tiun je redundanco por rekono aux korekto de eraroj, kaj ankaux la strebadon al simpleco. Kodoj kun "fiksita vorto-longeco", kie cxiu vorto aux signo estas egale longa, estas tre simple malkodeblaj, sed ne povas konsideri la oftecon de signoj por doni al oftaj signoj mallongan kodon. Tamen tiaj kodoj estas ofte uzataj; gxenerale la kodoj por komputilaj tekstoj, kia ISO 8859, estas de tiu speco.
Kiel dirite, la celo de cxifrado estas kasxi informon. Ni do uzu la difinon, ke cxifro estas kodo, per kiu oni celas kasxi la koditan informon.
La uzanto de cxifro do celas, male al kodo, lauxeble malfacilan malcxifradon, almenaux por aliaj, ne inicitaj. Kun la scio de la cxifro, la malcxifrado tamen estu ne tro malfacila.
La unua aplikado de cxifroj kredeble estis en armeoj, por teni militajn informojn sekretaj. Jam antaux 2000 jaroj Julio Cezaro uzis cxifron, kiam li sendis militajn ordonojn per mesagxisto. Tiu cxifro estis tre simpla: Anstataux cxiu litero li uzis la trian sekvantan en la alfabeto (komparu figuron 2, kaj [1, 11]).
| a | k | a | d | e | m | i | o | klara mesagxo |
| b | l | b | e | f | n | k | p | |
| c | m | c | f | g | o | l | q | |
| d | n | d | g | h | p | m | r | cxifrita mesagxo |
La celo de inform-kasxado gxenerale estas elstare grava cxe cxifroj, kaj cxiuj aliaj celoj cedas al gxi. La cxefa aux ecx unusola kriterio por la kvalito de cxifroj do estas la malfacileco de ilia solvado aux "rompado". Laux tiu kriterio, la cxifro de Cezaro certe ne estis tre bona; gxi estas facile atakebla per kripto-analizo, kiu rapide konstatus, ke kelkaj literoj, ekzemple r kaj z, okazas tre ofte, kaj ke z precipe okazas en la kombinoj zp kaj zx; el tio gxi konjektus, ke z=u, zp=um kaj zx=us ktp. (atentu, ke la latina alfabeto antaux 2000 jaroj ne posedis la literojn j kaj w, kaj identigis u kaj v).
| a | k | a | d | e | m | i | o | mesagxo | |
| + | i | n | t | e | r | n | a | c | cxifro-vorto (sxlosilo) |
| = | j | d | u | hx | v | f | j | s | cxifrita mesagxo |
Estas tre facile plibonigi la sekurecon de la cxifro de Cezaro, per la enkonduko de t. n. cxifro-vorto (sxlosilo). Anstataux sxovi cxiun literon je konstanta distanco en la alfabeto, do "adicii" al gxi konstantan nombron (ekz. 3), oni adicias al cxiu litero en la mesagxo la sampozician literon en la sxlosilo, kalkulante a=1, b=2, ...; komparu figuron 3. Post la fino de la sxlosilo oni reuzas gxin de la komenco. Ju pli longa la sxlosilo, des pli sekura tiu cxifro estas. Cezaro uzis la sxlosilon "c", konsistantan el nur unu litero.
Laux tiu metodo eblas konstrui ne-atakeblan cxifron, per la konstruado de cxifro-vorto same longa kiel la mesagxo. La nura kondicxo estas, ke tiu cxifro-vorto estu absolute hazarda; se oni elektus ekz. la tekston de iu libro, la cxifro denove farigxus atakebla.
Tre konata, ecx normigita [9] proceduro estas la DES-cxifro, kies nomo estas mallongigo de la angla nomo data encryption standard (daten-kriptiga normo). Gxi konsistas esence el jena skemo, liganta mesagxo-blokon m kaj sxlosilon s helpe de funkcio f (kp. [2, 11]):
Por DES ekzistas specialaj cirkvitoj,
kiuj plenumas la cxifradon tre rapide.
Ankaux ekzistas jam metodoj por rompi la cxifron,
kvankam kun granda elspezo;
pro tio la cxifro estas konsiderata ne plu tre sekura.
[11] indikas pli sekurajn variajxojn.
3 Juraj problemoj en komunikado
Bedauxrinde, en interhomaj rilatoj oni cxiam devas kalkuli
kun la interveno de "malbonulo",
kiu provas havigi al si nejustan avantagxon.
En komunikaj procezoj ekzistas certaj skemoj de tia interveno,
kontraux kiuj necesas protekto.
Esence temas pri la problemoj de spionado kaj falsado.
Kiam triaj personoj, mesagxistoj aux aliaj, provas akiri scion pri la enhavo de sekreta mesagxo, ni parolas pri spionado aux, kaze de parola komunikado, pri subauxskultado. Kontraux spionado de skriba mesagxo fare de mesagxisto aux aliaj protektas sxlosita valizo, aux sigelita koverto, kiu almenaux malhelpas nerimarkitan spionadon. Kaj, kompreneble, la protekto kontraux spionado estas la tradicia apliko de cxifrado.
Sxajnas do, kvazaux almenaux rilate spionadon ne estas granda diferenco inter la tradicia kaj la nova komunikado. Tamen ni memoru, ke cxifradon tradicie oni aplikas nur por tre gravaj aferoj, kaj ke ordinare ni fidas la protekton de gluita -- ecx ne sigelita -- koverto kaj la diskretecon de la posxto. Cxe grand-skala apliko de cxifroj montrigxas du gravaj problemoj:
Pro tiuj problemoj, la tradiciaj metodoj de cxifrado ne povas
senplue preni la rolon de kovertoj en la nova komunikado.
3.2 Falsado
Ofte ne tre gravas la sekreteco de mesagxo,
sed preskaux cxiam gxia gxusteco.
Ni supozu,
ke certa mesagxo de A al B temas pri gravaj aferoj,
tiel ke falsado havas seriozajn konsekvencojn.
Tiam povas okazi jenaj bazaj situacioj:
Evidente necesas rimedoj kontraux tiaj fiajxoj, alie ekestus tia necerteco en komercado, ke neniu plu fidus gravajn komunikajxojn. En la tradicia komunikado per paperaj dokumentoj oni procedas jene:
Cxar elektronika mesagxo ne havas materian substraton, ne eblas auxtentikigi gxin per specialaj papero, inko aux similajxoj. Ankaux identigiloj kiaj subskriboj, emblemoj kaj stampoj ne utilas, cxar en digxita formo ili estas sen ia malfacileco kopieblaj. Se iu fiulo C ekzemple posedas la subskribon de A sur telekopia dokumento, li povas kopii gxin en alian telekopian dokumenton kaj sendi tiun al B; B havas nenian sxancon konstati la falsadon, cxar la papero estas lia propra, el lia telekopiilo, kaj la subskribo estas nedistingeble la sama kiel tiu sur la auxtentika telekopio de A.
Pro tio, B havas neniun bazon por fidi al la telekopia dokumento, kaj li ne bazos sur gxin iujn gravajn, nemalfareblajn agojn, se li ne havas konfirmon el alia fonto.
4 Informacio
Por pli bone kompreni la funkciadon de kodoj
kaj la diferencon inter la tradicia kaj la nova komunikadoj,
ni bezonas mezuron por la inform-enhavo de mesagxo.
Tiu inform-enhavo nomigxas informacio.
Gxenerale oni uzas jenan difinon:
La informacio (inform-enhavo) de mesagxo estas
la nombro de binaraj decidoj (jes-ne-decidoj),
kiuj estas necesaj por rekonstrui la informon de la mesagxo.
Tia decido kiel mezur-unuo nomigxas bito.

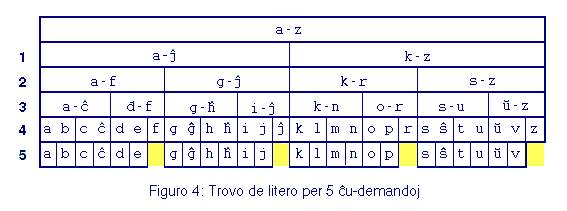
Figuro 4 montras, ke unu litero el la internacialingva alfabeto mezume enhavas informacion de malpli ol 5 bitoj: Laux la demando-skemo en la figuro eblas trovi la literon per maksimume 5 demandoj, parte jam post 4. Se cxiuj literoj estus egale oftaj, ni havus mezan bezonon de (24 * 5 + 4 * 4) / 28 ~ 4,86 demandoj. Se la nombro de signoj estas entjera potenco de 2, n = 2m, kaj se cxiuj signoj havas la egalan relativan oftecon (probablecon) p = 1/n, la per-duoniga demando-skemo estas optimuma kaj bezonas precize m decidojn; do la informacio de cxiu signo estas m = log2 n = - log2 p bitoj. Tiu formulo montrigxas gxeneraligebla ankaux al neegalaj oftecoj.
La meza informacio de signaro nomigxas ankaux gxia entropio (kp. [7]); analoge al la termodinamika entropio, gxi estas maksimuma, se la signoj estas egale probablaj. Gxi kalkuligxas kiel la sumo de la informacioj I de la signoj, pezigitaj (multiplikitaj) per sia probableco:
Se cxiu signo el 28 estas egale probabla, la entropio estas nur log2 28 ~ 4,81; gxi estas la suba limo por la decid-bezono de iu ajn demando-skemo (teoremo de Shannon).
La informacio en mesagxo dependas ne nur de la mesagxo mem,
sed ankaux de la inform-stato de la ricevanto.
Se li jam konas la enhavon de la mesagxo,
gxi portos al li nur malmulton novan, nome la fakton,
ke iu volas informi lin.

Figuro 5 montras simplan "lingvon" kun kvar literoj, kiuj do povus porti log2 4 = 2 bitojn. La plej simpla demando-skemo, cxiam duoniganta la signaron, do bezonas 2 decidojn; sed konsiderante la malsamajn oftecojn de la signoj, oni vidas ke la meza informacio de litero estas nur 1,75 bitoj. La sama fenomeno okazas en homaj lingvoj: Bauer kaj Goos [1] indikas por la germana lingvo kun 26 literoj (+ vorto-limo) mezan informacion de 4,11 bitoj, anstataux log2 27 = 4,75. Sherwood donas en [14, 15] la relativajn oftecojn de la fonemoj en konversacio en Esperanto; laux lia tabelo de du-fonemoj konkludeblas, ke la vorto-limo havis oftecon de cx. 15,2 %, simile kiel en la germana. El tio sekvas meza informacio de 4,10 bitoj / signo, anstataux log2 29 = 4,86 sen konsidero de la oftecoj.
La informacio en teksto farigxas malpli granda, se oni konsideras grupojn de sinsekvaj literoj, cxar evidente la ofteco de litero dependas de la antauxa. Ekzemple en multaj euxropaj lingvoj la litero q estas preskaux cxiam sekvata de u; en Esperanto, post h, v aux z preskaux cxiam sekvas vokalo. La datenoj de Sherwood el [15] por paroj de fonemoj (kiuj kredeble estas similaj al paroj de literoj) kondukas al informacio de nur 3,7 bitoj / litero; mezume do cxiu litero perdas dekonon de sia informo per tio, ke la leganto jam scias la antauxan. (Tiuj datenoj ne estas tute kompareblaj kun datenoj por skribita teksto, cxar Sherwood laux prononca vidpunkto distingas kroman pauxzo-fonemon (ekz. inter n-k), kiu ne havas skriban respondajxon. Se konsideri tiun fonemon ankaux por la kalkulo kun unuopaj fonemoj, la entropio en tiu 30-fonema alfabeto (28 + vorto-limo + pauxzo) estas ne 4,10, sed 4,19 bitoj.) Konsidero de pli longaj grupoj plu malgrandigas la informacion: la unua eldono de [1] indikas por la germana lingvo redundancon de almenaux 66 %; la kvara eldono indikas minumume 80 % sen konsidero de la enhavo. (Tio signifas, ke cxiu litero portas nur cx. 1 biton.)
Kodoj, kiuj konsideras la oftecon de signoj, havas malpli da redundanco, do bezonas malpli da spaco. En kelkaj okazoj, kiam spaco aux transsendo-tempo kostas pli ol alir-tempo, tio povas esti utila. Huffman indikis optimuman kodadon de la latina alfabeto por la oftecoj de mezumaj anglaj tekstoj, en kiu la literoj E kaj T okupas nur po tri, kontrauxe Q kaj Z po dek-unu bitojn (kp. [1]). La plej uzataj kunprem-algoritmoj tamen ne supozas iun fiksitan probablecon de signoj, sed esploras la donitan tekston por trovi kodo-tabelon optimuman por ties probablo-denseco. Male al la uzo de fiksa kodo-tabelo, cxi tie necesas stori ankaux la tabelon, sed cxar kunpremado kutime estas aplikata al grandaj datenaroj, tio ne estas grava.
Eble la plej uzata kunprema algoritmo estas la kunpremado por telekopiaj mesagxoj. Ordinara A4-pagxo skanita per difino de 200/colo (~ 8/mm) donas bild-informon de preskaux 4 milion bitoj, el kiuj la blankaj kaj la nigraj ofte formas pli aux malpli grandajn kunligitajn areojn. Tiuj areoj, precipe la nigraj, ofte estas malgrandaj aux havas mallargxejojn. Pro tio telekopiiloj kunpremas la informon
Per tiu algoritmo,
ordinara tajpita pagxo bezonas anstataux 4.000.000 bitoj
malpli ol dekonon de tio.
Tio grave reduktas la kostojn kaj tempon por telekopiado.
La redukto kompreneble dependas de la enhavo de la pagxo.
5 La noveco de la nova komunikado
La koncepto de informacio ebligas formuli la kredeble esencan diferencon de la novaj komunikaj teknikoj disde la tradiciaj.
Kiel jam menciite, grava diferenco estas la manko de materia substrato cxe la elektra komunikado, substrato, kiu povas servi por malfaciligi la produktadon de simila (falsita) komunikajxo, kaj kiu povas registri spurojn de eventuala falsado. Tio tamen ne estas la sola, eble ecx ne la plej grava diferenco: Ekzemple la subskribo de homo estas konsiderata kiel auxtentika sendepende de la uzata papero aux skribilo.
La rolo de la materia substrato cxefe estas la ligo inter la komunikajxo kaj la auxtentikigilo: subskribo au stampo legitimas nur la mesagxon, kiu estas sur la sama folio, kaj en kiun penetris gxia inko. Subskribo sur aparta folio, aux kopiita sur alian folion, ne estas valida.
Same grave estas tamen, ke la informacio en subskribo aux stampo ne estas precize kaptebla: Ecx la plej detala analizo de falsanto ne povas esti certa, ke gxi kaptis la tutan strukturon, kaj ke alia analizo ne estos pli detala kaj malkovros la falsadon. Tiun fakton, ke analizo je cxiu skalo trovas esence la saman kompleksecon, oni nomas frakteco. Subskribo aux stampo do estas frakta objekto, kaj tio signifas, ke ecx la plej fidela falsado ne povas esti absolute certa, ke gxi ne estos rimarkita.
Figuro 8 montras diversajn nivelojn de detaleco laux la ekzemplo de stampo. La produktanto de la auxtentika stampilo devas okupigxi nur pri la unuaj tri niveloj; sed se falsanto imitas nur tiujn, komparo kun auxtentika stampo rivelos diferencojn sur la kvara aux almenaux la kvina nivelo.
Digxita komunikajxo ne povas esti frakta; gxia informacio estas absolute klare fiksita. Por gxia auxtentikigo necesas io, kio estas digxita kaj tamen (praktike) neimitebla.
Tio signifas aliflanke, ke la analizo de digxita auxtentigilo -- ni nomu gxin digxita subskribo (komparu la antauxan rimarkigon) -- estas absolute certa afero: Ne povas esti dubo pri gxia valideco aux nevalideco. Kaj ne necesas esti spertulo pri manskriboj, paperoj aux inkoj por prijugxi gxin.
Resume ni povas diri, ke metodo por digxita subskribo devas plenumi jenajn kondicxojn:
La solvo por cxiuj menciitaj problemoj de la nova komunikado kusxas en la ideo de nesimetriaj, unu-direktaj cxifroj. Unu-direkta cxifro (ankaux nomata "klap-porda cxifro", aux "klap-porda funkcio", kp. [10]) estas cxifro, kies mal-cxifro estas ege malfacile (do praktike ne) kalkulebla ecx por tiu, kiu perfekte konas la cxifron. La ideo utiligi tiajn cxifrojn unue estis proponita de Diffie kaj Hellman [4].
| B cxifras per PA | ----------- > C ne povas spioni |
A legas per SA | < ---------- B ne povas spioni |
C cxifras per PA |
Iu persono povus do "posedi" tian unu-direktan cxifron kaj gxian malcxifron kaj publike konigi la cxifron; tamen neniu povus eltrovi la malcxifron, kiu restus privata posedajxo. Tiamaniere cxiu povus sendi al tiu persono cxifritan mesagxon, kiun neniu tria persono povus legi, kaj tamen nur unu kodo estus necesa (kp. figuron 9). Do jam por nura sekretigo de mesagxoj tiaj unu-direktaj cxifroj estas ege utilaj.
La du erojn de tia cxifro, la privatan kaj la publike konatan, oni nomas sekreta (privata) sxlosilo kaj publika sxlosilo, cxar kutime temas nur pri sxlosil-nombroj aux -vortoj, enmetataj en iun gxenerale aplikeblan skemon. Posedanto de cxifro do povas diskonigi la publikan sxlosilon, sed devas bone gardi la privatan.
Por tio estas grave, ke la cxifritaj mesagxoj uzu la saman alfabeton kiel la klaraj, kaj ke la cxifraj funkcioj dujxete bildigu la aron de la eblaj mesagxoj al gxi mem. En tiu kazo, la du sxlosiloj P kaj S operacias komute:
S o P = Id
(P o S) o (P o S) =
P o (S o P) o S =
P o Id o S = P o S
P o S dujxeta (inversigebla) == >
S o P = Id = P o S
do, ne nur el cxifrado kaj posta malcxifrado rezultas identeco, sed ankaux el malcxifrado (= cxifrado per S) kaj posta cxifrado (= malcxifrado per P). Per tio eblas, ke A sendas mesagxon cxifritan per sia SA, kiujn la adresato malcxifras per la publike konata PA.
Tia mesagxo cxifrita per SA (t. e. malcxifrebla per PA) povas nekontesteble veni nur de A; ja neniu alia scias SA. Kaj tiu auxtentigilo estas intime ligita kun la mesagxo; la mesagxo mem ja estas konstruebla el gxi. Do tiu cxifrado per privata (sekreta) sxlosilo SA plenumas gxuste la du kondicxojn de la fino de cxapitro 5 por digxita subskribo.
Tiu ideo, cxifri mesagxojn per cxifro, kies solvon (la publikan sxlosilon) cxiu konas, estas la bazo de la koncepto de digxita subskribo: Cxar cxiu konas la solvon de la cxifro, cxiu povas kontroli la auxtentikecon de la subskribo; sed cxar neniu povas imiti la cxifradon, neniu povas falsi alies subskribon.
Estu n natura nombro, produto de du primoj, n = pq, kaj c, d el N tiaj, ke [ cd mod (p-1)(q-1) ] = 1. Tiam, laux la malgranda teoremo de Fermat, por cxiu natura nombro a validas
(acx)d = acd == a mod n
Do la nombroj c kaj d estas uzeblaj kiel cxifro kaj malcxifro: Oni cxifras la mesagxon a per c-potencigo module de n, la rezulton oni malcxifras per d-potencigo module de n. Komuna al ambaux procezoj estas nur la scio de n.
La decida eco de la metodo estas, ke por derivi d el c kaj n necesas trovi la nombrojn p kaj q, do faktorigi n, kio postulas multe pli grandan laboron ol la cxifrado mem, kaj ke tiu laboro kreskas superlineare kun n. Se do la elektitaj p kaj q estas tiom grandaj, ke la faktorigo ne eblas en, ni diru, kelkaj jarcentoj, la cxifrado per c estas praktike ne-inversigebla -- gxi estas klap-porda funkcio.
Por pli bone kompreni la praktikan funkciadon de la metodo, ni rigardu ekzemplon kun malgrandaj, tamen ne tro malgrandaj nombroj. Mi elektis tiajn, ke la kalkulado estas ankoraux sen granda peno farebla per posx-kalkulilo, kaj indikis la inter-rezultojn por tiuj, kiuj volas lauxfari la kalkuladon:
| p: | 11 | unua primo |
| q: | 17 | dua primo |
| n = pq = | 187 | |
| (p-1)(q-1) = | 160 | |
| 7 * 23 = | 161 | = 1 mod (p-1)(q-1), do |
| c: | 7 | publika sxlosilo |
| d: | 23 | sekreta / privata sxlosilo |
Se ni volas sendi al la posedanto de la cxifro la mesagxon a = 24, ni do devas kalkuli ax mod n = 247 mod 187:
247 = 244 * 243 = 331776 * 13824 247 = 38 * 173 mod 187 = 29 mod 187
Ni do sendas al la adresato la cxifritan mesagxon 29, kaj li malcxifras gxin per sia sekreta sxlosilo d = 23:
2923 = 294 * 294 * 294 * 294 * 294 * 293
2923 = 47 * 47 * 47 * 47 * 47 * 79 mod 187
= 38 * 40 mod 187 = 24 mod 187
Jam tiu malgranda ekzemplo montras, ke ne estas tute facile trovi la sekretan sxlosilon SA = d = 23 el n = 187 kaj la publika sxlosilo PA = c = 7.
Ideale estus, se ajna modifo de la teksto sxangxus la kontrol-valoron, sed evidente tio ne povas esti, cxar la kontrol-valoro estas ja malpli longa ol ordinaraj mesagxoj. Tamen h devas esti tia, ke ne estas facile por falsanto fari modifon al m, kiu ne sxangxas la kontrol-sumon. Pro tio ekzemple ne eblas, ke h simple estu la sumo de la kodoj de cxiuj literoj en m, cxar tiam falsanto ja povus libere sxangxi la ordon de la literoj.
La uzata h estu la sama por cxiuj, cxar sendanto kaj ricevanto de m ja ambaux devas apliki la saman, por subskribi kaj por kontroli. Se iu uzus sian propran funkcion, li devus unue komuniki gxin per sekura vojo al siaj korespondantoj; alie falsanto povus aldoni al falsita mesagxo ankaux falsitan h, kiu donus la gxustan subskribon. [3] rekomendas jenan algoritmon:
dividu la mesagxon m en partojn ai de po 256 bitoj
kompletigu cxiun parton per antauxmeto de 256 1-bitoj al bi
kalkulu h := (...((b1 AUX b2)2 AUX b3)2 AUX ... AUX bn)2
(AUX estas la lauxbita elkluda aux-funkcio)
Se A volas sendi al B la subskribitan kaj sekretan mesagxon m, la procedo estas jena:
Krome A bezonas komputilan programon, kiu faras la cxifradon kaj malcxifradon, kiuj ne estas fareblaj sen masxina helpo. Tiu programo povas esti identa por cxiuj, kaj cxiu povas uzi gxin per sia privata sxlosilo, aux per la publika sxlosilo de aliaj.
Laste, A devas teni liston de la publikaj sxlosiloj de siaj korespondantoj, por ke li povu sendi al ili cxifritajn mesagxojn kaj kontroli iliajn subskribojn. Tiun liston li devas bone gardi kontraux modifoj de eksteruloj!
Se F volas gxeni la komunikadon inter A kaj B, li substituus al la publika sxlosilo PB en la listo de A iun PF, kies SF li mem konas. Tiam li povas sendi al A subskribitajn leterojn, kiujn A akceptos kiel auxtentikajn leterojn de B; same F povas per SF legi la sekvan leteron de A al B, cxar A cxifris gxin per la substituita PF. Cxar la adresato B mem ne povas legi la leteron, li kredeble protestos cxe A, kaj tiam A rimarkos, ke iu falsis lian liston; sed eble la malutilo jam okazis.
Evidente estas dangxere administri simplan liston de siaj korespondantoj kun ties publikaj sxlosiloj, cxar ecx la plej eta dubo pri modifo fare de eksterulo detruas la fidon en la tuta sistemo. Pro tio estas pli bone, ke ne cxiu unuope tenu liston, sed ke la publikaj sxlosiloj trovigxu en "katalogo" (masxine legebla) simila al telefon-libro, eldonata de iu fidinda centra instanco aux auxtoritato, nomata certiga auxtoritato (CA). Pri la organizado de CA ekzistas rekomendo de la Konsulta Komitato Internacia pri Telegrafio kaj Telefonio [3].
Evidente ankaux la katalogo estas en dangxero de falsado; falsanto povus eldoni falsitajn katalogojn aux modifi ekzistantajn. Do necesas certigi ankaux la katalogon per digxita subskribo, nome per tiu de la certiga instanco.
Grave estas, ke la certiga auxtoritato ne devas stori, ecx ne scii la privatajn sxlosilojn. Se iu petas la registradon kaj konfirmadon de iu publika sxlosilo, ne gravas cxu li posedas la respondan privatan; la malavantagxo estos lia propra, kiam li ricevos mesagxon, kiujn li ne povas malcxifri. Sed cxar la CA ne scias la sekretajn sxlosilojn, ili tie ne estas en dangxero de malkasxo.
La registrado do koncernas sole la publikan sxlosilon. Kiu volas registrigi sxlosilon kaj akiri por gxi certigilon, ne bezonas pruvi ke li scias la respondan privatan sxlosilon (kvankam tia pruvo eblas sen malkasxo de la sxlosilo mem; suficxas doni subskribon al kelkaj prezentitaj tekstoj). Certigilo por iu publika sxlosilo neniom utilas sen scio de la privata sxlosilo: Oni eble ricevos mesagxojn, kiujn oni ne povas malcxifri, kaj se iu alia scias la privatan sxlosilon, oni ecx devas respondeci por ties subskriboj!
Por kompreni tiun fakton necesas klarigi al si, ke la akiro de certigilo pri iu certa sxlosilo estas malavantagxo -- gxi devigas akcepti la respondecon pri la koncernaj subskriboj. La avantagxo, kiun oni akiras per la certigilo, estas la posedo de iu ajn sxlosilo; tiu posedo ebligas la intersxangxon de auxtentikigitaj mesagxoj. La registrado de iu certa sxlosilo portas nur respondecon kaj estas malutila, se iu alia scias la respondan privatan sxlosilon. Pro tio estas afero de la petanto de certigilo, zorgi ke li registrigu la gxustan sxlosilon. Se li registrigas publikan sxlosilon sen scio de la privata, estas lia propra kulpo.
Kutime certigilo enhavas pliajn indikojn, ekz. la realan kaj komputil-posxtan adresojn de la posedanto kaj ofte daton de malvalidigxo. Cxi tio estas pasxo por limigi la damagxon en la okazo, ke la sekreta sxlosilo erare farigxas konata al alia persono. Tiam iu, kiu misuzas la cxifron kaj gxian certigilon, almenaux povas tion fari nur dum certa tempo, cxar la posedanto ja ne plilongigas la validecon.
Antaux doni certigilon, la auxtoritato devas plej severe kontroli la identecon de la petanto. Egale cxu tiu persone aux letere faras la peton, zorga auxtentikigo estas nepra. Kontrauxe ne necesas zorgo cxe la resendo de la certigilo, cxar gxi ja aperos en la publika katalogo.
Cxar la primoj p kaj q malantaux la sxlosiloj devas esti longaj (almenaux 100 ciferojn), ankaux la privataj sxlosiloj estas tiom longaj, ke la plej multaj homoj ne povas memori ilin; krome estus tede, entajpi ilin antaux cxiu uzo. Tial necesas stori sian privatan sxlosilon en masxine legebla formo. Plej bone estas stori gxin en malgranda objekto, kiun oni facile portas cxiam kun si. Por tio servas la tiel nomataj "ico-kartoj", malgrandaj komputiloj en la formato de cxek-karto (kp. [2]). Ili enhavas storon por la sxlosilo (kaj eble aliaj aferoj) kaj procezilon por la cxifrado. Tiel la sxlosilo mem neniam bezonas eliri el la karto; por uzado oni konektas la karton al iu komputilo (enmetas gxin en konektingon), kiu donas al gxi nombron kaj rericevas la cxifritan nombron.
Multe malpli sekure estas stori la sxlosilon en loke fiksita komputilo, kies aliro ne estas facile kontrolebla, kaj kiu estas libere programebla. Tamen ankaux la ico-karto ne estas perfekte sekura, cxar eblas perdi, sxteli aux ecx nerimarkate misuzi gxin. Tial nepre necesas plia sekurigo en la formo de persona identiga numero (PIN), cxirkaux kvar aux kvin ciferojn longa, storata nenie, kiun la posedanto devas memori kaj entajpi antaux cxiu uzo de la sxlosilo, same kiel cxe bank-auxtomata karto. La procezilo en la ico-karto kontrolas la gxustecon de la entajpita numero kaj sxlosas la karton kontraux plua uzo, se tri sinsekvaj provoj estas malgxustaj.
La persona ico-karto estas ankaux tauxga loko por stori la publikan sxlosilon de la plej ofte uzata CA; ankaux tiu sxlosilo ja devas esti gardata kontraux modifoj.
Cxu la sxlosilo estas generata de la CA cxu de la kliento, ambauxkaze devas enveni iu pure hazarda influo, por ke la trovitaj p, q ne estu postkalkuleblaj fare de eksterulo. Se iu povus kalkuli, kiujn sxlosilojn iu CA vendis dum iu tago, li povus per eksperimentado eltrovi la sxlosilojn de cxiuj, kiuj je tiu tago acxetis sxlosilon de la CA. Same tiu, kiu mem kalkulas per iu programo siajn sxlosilojn, devas apliki iun hazardan influon, por ke ne cxiuj uzantoj de la sama programo trovu la samajn sxlosilojn. Tia hazarda elemento devas esti perfekte neimitebla, kiel la falo de jxetkubo, kaj gxi devas havi vastan gamon da eblaj valoroj, por ke neniu povu traprovi cxiujn eblajn valorojn.
Per tio cxiuj dokumentoj subskribitaj per tiu sxlosilo perdas sian validecon! Tial tiu pasxo estas ekstrema rimedo, aplikata nur en okazoj de vera dangxero.
Kial ankaux malnovaj dokumentoj perdas sian validecon post la revoko de la sxlosilo? Cxar ja ne eblas pruvi, ke la dokumento estis subskribita antaux la revoko. Se la dokumento enhavas daton, ankaux tiu dato ja povas esti falsita.
Escepto estas, kiam la dokumento kun subskribo estas konfirmita de tria instanco, per ties ne-perfidita sxlosilo, je iu dato, kiam la perfidita sxlosilo estis ankoraux sekura. Tiam tiu dokumento postvivas la perfidon de la origina subskribo. Pro tio estas rekomendinde, por tre gravaj dokumentoj akiri konfirmon de iu fidinda instanco, ekzemple notario.
Vera problemo okazas, kiam la sxlosilo de iu CA estas perfidita. Evidente tio malvalidigas ankaux cxiujn certigilojn donitajn de tiu CA; tamen gxi ne tusxas la konfirmitajn sxlosilojn, por kiuj eblas akiri novan certigilon. Sed se la posedanto A de iu sxlosilo rifuzas akiri tian, iu posedanto B de dokumento subskribita de A ne povas pruvi ties auxtentikecon, escepte se li gxustatempe akiris konfirmon por tiu dokumento.
Pli subtila atako estas, provizi iun per malgxustaj informoj pri alies sxlosiloj. Tial oni fidu nur sxlosilojn, kies certigilo estas disponebla, kaj oni kontrolu la certigilon cxe cxiu uzo.
Aparta problemo estas la ebleco revoki sian sxlosilon (pretendante ke gxi estas perfidita) kaj dementi gravan dokumenton. Cxar la revoko de sxlosilo ne nur kauxzas multajn problemojn por la posedanto, sed ankaux malutilas al lia reputacio kaj fidindeco, certe neniu faros tian trompon pro bagatela avantagxo, sed nur pro tre grava profito. Kontraux tio helpas nur, akiri notariajn konfirmojn pri la tempo de cxiuj gravaj negocaj subskriboj.
Variajxo de cxi-lasta estas transdoni sian privatan
sxlosilon al iu komplico,
kiu registrigas gxin kiel sian, asertante ke li mem kalkulis gxin;
tiam la du komplicoj povus cxiam pretendi ke iun
gravan subskribon donis la alia.
Pro la malgranda probableco, ke du personoj trovu la saman sxlosilon,
tia okazo estas nekredinda kaj suspektinda.
7 Perspektivo
Ni montris,
ke unu-direktaj cxifroj tauxgas kaj por sekretigo
kaj por auxtentikigo de digxitaj mesagxoj,
ke la metodo de digxita subskribo estas tauxga por
doni al digxitaj komunikajxoj similan gradon de fidindeco kiel
al tradiciaj.
Lige kun la pli grandaj rapideco kaj komforto de
digxita komunikado,
tio certe kontribuos al ties pli vasta uzo.
La gxenerala apliko de tiuj metodoj necesigas ankaux sxangxon en la konscio de la uzantoj, kiuj devas kutimigxi doni al digxita subskribo la saman fidon kiel al tradicia, sed ankaux respekti la privatecon de alies ico-karto kaj PIN.
Al interesuloj mi rekomendas por legado la tre inform-ricxan libron de Jaburek [11] (en la germana), kaj la tie indikitan literaturon. Pri ico-kartoj informas la libro de Beutelspacher k. a. [2].