Sekureco kaj konfidenceco en komputila komunikado
Kontraste al la tradicia komunikado parola aŭ letera ni distingu "novan" komunikadon, kiu okazas per la novaj komunikiloj de retpoŝto, telekopio (faksado), teletajpado ktp. Kontraste al la tradiciaj komunikiloj en la novaj normale ne estas materia substrato por la mesaĝo, kiu estas materie sendata; transportata estas nur informo. Tiu informo normale vojaĝas en cifereca formo, ne en analoga kiel ĉe tradiciaj telefono aŭ radio.
La nocioj "informo" kaj "scio" estas parencaj, tial eblas supozi, ke aŭtentikigo per scio estas bone uzebla en nova komunikado.
Multaj bankoj proponas al siaj privataj klientoj "ciferecan bankadon", do administradon de la propra konto (precipe ĝiroj) pere de komputilo kaj ret-konekto (iam ankaŭ per rekta telefon-ligo). Kontraste al tradicia bankado per paperaj formularoj mankas la sekureco de presita, ne sen peno imitebla formularo kaj precipe la aŭtentikigo per subskribo. Do ekestas pluraj problemoj:
La komunika situacio en la ekzemplo ne estas kontentiga. Analizante la komunikan procezon oni trovas du kialojn por tio.
La ekzemplo pri la banko montras du eblojn, aŭtentikigi mesaĝon per informo: Oni kunsendas interkonsentitan sekretan informojn, kiu povas esti konstanta, ripete uzata (PIN) aŭ ŝanĝiĝanta, unufoje uzata (TAN). La dua maniero estas pli sekura kontraŭ spionado (subaŭskultado), sed neniu protektas kontraŭ malhonesta sendanto aŭ ricevanto. Se, en la ekzemplo, la kliento asertas, ke li sendis ĝir-komision al firmao X, kaj la banko asertas, ke ĝi ricevis komision al firmao Y, neniu povas pruvi ion.
La kaŭzo estas, ke oni ne vere aŭtentikigas mesaĝojn. Per PIN-o aŭ TAN-o la kliento ne diras "mi aŭtentikigas mian ĝir-komision", sed "mi pruvas mian identecon" (al la banko). Tiu situacio jam tradicie ekzistis ĉe parolaj ("buŝaj") mesaĝoj. Tion montras jena sceno el romano (Karl May: "En la ravinoj de l' Balkano"):
|
"Tiam estus bone, se via frato same fidus al mi." "Li fidos, ĉar sendas vin mi." "Ĉu vi ne povus doni al mi kelkajn liniojn por li?" "Mi ne scipovas skribi. Sed ... diru al li, ke sendas vin lia duonfrato. Neniu scias, ke ni havis malsamajn patrinojn. Kiam mi sendas al li konfidencan mesaĝon, la duonfrateco ĉiam estas signo, ke li fidu la mesaĝulon." |
Tiu teksto klare diras, ke la sekreto pruvas, ke la mesaĝulo estas fidinda. Ĝi legitimas personon, ne mesaĝon. Per tia sekreto ne eblas aŭtentikigi certan mesaĝon. La problemo estas, ke ne eblas ligi la aŭtentikigilon al la mesaĝo, kiel oni ligas subskribon aŭ stampon al la papero de skriba mesaĝo.
Pro tiu kaŭzo subskribo sur kopiitan (fotokopiita, telekopiita) mesaĝo valoras nenion: La ligo inter ĝi kaj la mesaĝo perdiĝis dum la kopiado, la papero estas alia. Ne eblas pruvi, ke la kopiitan mesaĝo ne estis kunmetita el du pecoj (falsita teksto kaj subskribo kopiita de alia mesaĝo).
Eĉ se TAN-o ne pruvas, ke kliento sendis certan mesaĝon, ĉu ĝi ne pruvas almenaŭ ke li entute sendis mesaĝon? Bedaŭrinde ne, ĉar la TAN-oj ja originas de la banko; la fakto, ke ĝi posedas (scias) iun TAN-on ne pruvas, ke kliento sendis ĝin. Kaj por kontroli la ĝustecon de iu TAN-o la banko ja bezonas la liston de la TAN-oj.
Tiun lastan fakton oni povus ŝanĝi, se la liston de la TAN-oj la kliento ricevus de alia, tria partio, iu neŭtrala TAN-instanco. Tiam la banko devus demandi tiun instancon, ĉu iu ricevita TAN-o estas vera kaj valida. Tio solvas parton de la problemo, sed ne vere, ĉar nun necesas simple fidi ne la bankon, sed la TAN-instancon.
En tradicia komunikado, kontraŭe, kontroli subskribon povas ĉiu, eĉ se li mem ne kapablas produkti tiun subskribon; kaj por kontroli stampon aŭ sigelon ne necesas la stampilo resp. la sigelilo.
Ĉu ne eblas pruvi la scion de sekreto sen malkaŝi la sekreton? Ekzistas fama historia ekzemplo por tio. En la 16-a jarcento la itala matematikisto Niccoló Tartaglia (1499–1557) trovis formulon por solvi triagradajn polinomajn ekvaciojn. Li do povis solvi problemojn de jena formo:
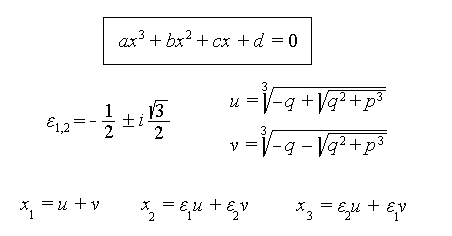
La unua linio montras la ĝeneralan formon de triagrada polinomo. La aliaj linioj montras, kiel eblas kalkuli solvojn por tiaj problemoj. Tartaglia estis do la sola homo, kiu sciis tiun solvo-metodon, ĉar li unue malkaŝis la metodon al neniu. Ĝi do estis lia sekreto.
Tamen Tartaglia povis pruvi, ke li posedas tiun sekreton! Li kapablis solvi ĉiun triagradan polinomon prezentatan al li, kaj li estis la sola homo, kiu kapablis tion fari. (Li poste malkaŝis la formulon al sia kolego Girolamo Cardano, sub kies nomo ĝi estas konata.) La kontrolo de tia solvo x estas facila: Oni kalkulas (ekzemple) la duan kaj trian potencojn de x, enmetas ilin en la polinomon kaj kontrolas, ĉu la rezulto estas 0 (nul). Jen ekzemplo: La donita polinomo estas
| x3 − 21 x2 + 146 x − 336 = 0 |
Solvi la polinomon ne estas facile, se oni ne posedas la formulon de Tartaglia/Cardano. Sed se iu asertas, ke "7" estas solvo de la problemo, estas facile kontroli tion:
|
73 −
21*72 +
146*7 −
336 =
343 − 21*49 + 146*7 − 336 = 343 − 1029 + 1022 − 336 = 0 |
Kontraŭe, se iu asertas, ke "5" estas solvo, eblas kontroli jene por konstati, ke tio ne estas vera:
|
53 −
21*52 +
146*5 −
336 =
125 − 21*25 + 146*5 − 336 = 125 − 525 + 730 − 336 = −6 |
Decida afero estas, ke Tartaglia povis solvi polinomojn, kiujn prezentis al li aliaj homoj. Se li nur prezentus solvon de polinomoj, kiujn li mem elektis, tio pruvus nenion, ĉar tiam li povus unue elekti la solvojn kaj el ili konstrui la polinomojn, kio estas facila afero. (Tiel ekestis la polinomo el la supra ekzemplo: Ĝi egalas al (x − 6)(x − 7)(x − 8).)
La sekreto de Tartaglia do montras, ke oni povas pruvi la posedon de sekreto, sen malkaŝi la sekreton. Tio funkcias, se io estas malfacile kalkulebla, sed facile kontrolebla.
La priskribita tekniko do (principe) solvas la problemon prezentitan en sekcio 4.2.2.
Ni vidis, ke Tartaglia povis per sia sekreto aŭtentikigi sin mem. Sed ĉu li povis aŭtentikigi ankaŭ mesaĝon? Li verŝajne ne faris tion, sed li estus povinta fari.
Por tio unue necesas transformi la mesaĝon al nombro. Tio estas facila; oni povas ekzemple numeri la literojn de la alfabeto (a = 01, b = 02, c = 03, ktp.) kaj vicigi la (duciferajn) nombrojn (aba = 010201). Se Tartaglia volus aŭtentikigi mesaĝon el literoj, li povus dividi la vicon en kvar partojn, transformi ilin al kvar nombroj a, b, c kaj d kaj konstrui el ili polinomon. La solvojn de tiu polinomo li povus kalkuli kaj sendi kune kun la mesaĝo al amiko, kiu povas kontroli la ĝustecon de la solvoj. Iu alia, kiu ne scias la sekretan formulon, ne povus kalkuli la solvon. La solvo do estas pruvo, ke la mesaĝo vere venas de Tartaglia.
La solvo estas kvazaŭ subskribo de la mesaĝo. Mesaĝo kaj subskribo estas matematike ligitaj per la fakto, ke la subskribo solvas la polinomon, kiun oni povas konstrui el la mesaĝo. Tiu ligo funkcias analoge al la papero, kiu ligas leteran mesaĝon al inka subskribo.
La priskribita tekniko do (principe) solvas la problemon prezentitan en sekcio 4.2.1.