Sekureco kaj konfidenceco en komputila komunikado
Por sendi ĉifritajn mesaĝojn kaj kontroli alies ciferecajn subskribojn oni bezonas la publikajn ŝlosilojn de aliaj homoj (aŭ instancoj). Oni povus konservi ilin en sia komputilo aŭ akiri ilin tra komputil-reto, sed ambaŭ metodoj havas malavantaĝojn:
La akiro de ŝlosiloj tra reto ne estas malbona ideo, sed necesas protekto kontraŭ falsado. Por tio ĉiu posedanto de ŝlosil(par)o akiru por sia publika ŝlosilo certigilo (konfirmilon) de agnoskita instanco, tiel nomata certiga aŭtoritato (CA). Tia certigilo estas dokumento, kiu enhavas la nomon (kaj aliajn identigilojn) de la posedanto kaj lian publikan ŝlosilon kaj estas ciferece subskribita de la CA. Tiam necesas nur la publika ŝlosilo de la CA por kontroli la aŭtentikecon de la certigilo kaj tiel la ĝustecon de la ŝslosilo.
La publika ŝlosilo de la CA devas veni el absolute fidinda fonto. Normale oni konservu ĝin en sia ico-karto, kune kun sia propra privata ŝlosilo.
Povas ekzisti multaj certigaj aŭtoritatoj, kaj ĉiu posedanto de ŝlosilo povas elekti sian. Ĉu tio signifas, ke necesas havi la publikajn ŝlosilojn de ĉiuj aŭtoritatoj en sia ico-karto? Ne. La aŭtoritatoj donas al si reciproke certigilojn por siaj ŝlosiloj, kaj A povas kontroli la ŝlosilon de iu persono B, kiu havas alian CA ol A, pere de la certigilo de B (subskribita de la CA de B) kaj de la certigilo de tiu CA, subskribita de la CA de A. Ties publikan ŝlosilon A ja havas en sia ico-karto.
En kelkaj landoj estas apartaj leĝoj pri CA-oj; ili preskribas ekzemple, kiel CA-oj protektu siajn datenojn.
Principe cifereca subskribo povas servi al ĉiuj transakcioj, kiuj nun necesigas paperan subskribon. Eblas per ĝi konfirmi mendojn, pagojn, ĝirojn, sed ankaŭ geedziĝon.
Kontraŭe al papera subskribo, la aŭtentikeco de cifereca subskribo estas kontrolebla de ĉiu kaj je ĉiu tempo. Ĝi do donas pli altan gradon de fidindeco ol mana subskribo.
En socio, kiu plene adoptis ciferecajn subskribojn, ĉiu plenkreska homo havus ŝlosil-paron. Tiun ne nepre devas generi iu aŭtoritato; tion povas fari ĉiu ajn, kiu havas taŭgan programon. Necesas kontroli la fidindecon de la programo; falsita (modifita) programo ja povus generi ŝlosilojn, kiujn ĝia aŭtoro jam konas. Tial la genera programo devas mem esti ciferece subskribita, ekzemple de ŝtata instanco, aŭ de fidinda CA.
Kun la helpo de tia programo adoleskanto povus (kial ne dum eta ceremonio aŭ festo?) generi sian propran ŝlosilparon kaj poste ĉe iu CA akiri certigilon pri ĝi. Por ke la generado ne estu imitebla, necesas provizi kelkajn hazardajn nombrojn. Ili estas facile produkteblaj per iuj pli-malpli hazardaj movoj de komputila muso. (Tiu musmovado povus esti grava parto de la ceremonieto.)
Interesa demando estas, ĉ necesas prezenti al la CA sian privatan ŝlosilon, por ricevi certigilon pri la publika. Principe tio ne necesas, kaj la privata ŝlosilo estu absolute sekreta, eĉ al la CA. Oni do teorie povus registri publikan ŝlosilon, kies privatan ŝlosilon oni ne scias. Sed kiu farus tion? Ne sciante la privatan ŝlosilon oni ne havas utilon de la registrado.
Kion iu CA faru, se iu petas certigilon por publika ŝlosilo, kiun jam registris iu alia? Ĉar estas ekstreme malprobable, ke du homoj generis la saman ŝlosilon, estas supozinde, ke la dua petanto kopiis la publikan ŝlosilon de la unua kaj ne vere posedas la privatan ŝlosilon, eble por ŝerco. Por malhelpi tiujn ŝercojn la CA povus peti, ke la certigilon oni petu per letero, subskribita per la privata ŝlosilo de la registrota paro.
Ofte estas grava la fakto, ke ciferecaj dokumentoj ne povas esti unikaĵoj; oni jam povas senprobleme kopii ilin. Tial estas ekzemple malfacile, oficiale forpreni de iu la ciferecan konduk-permesilon; eble li ja jam faris kopiojn. La sama problemo malfaciligas la uzon de ciferecaj ĉekoj; kopiojn de la sama ĉeko ja povus samtempe prezenti al diversaj bankoj diversaj personoj. Tial estas pli bone uzi ciferecajn ĝirilojn, kiuj enhavas la nomon de la ricevanto.
Alia apliko de subskriboj koncernas temon tre gravan por ĉiuj komputil-uzantoj, eĉ se ili ne aplikas elektronikan komercadon: Praktike ĉiuj personaj komputiloj estas minacataj de virusoj. Viruso-detektaj programoj ja donas certan protekton, sed la plej bona protekto estas rifuzo de programoj kaj dokumentoj, kies origino estas nekonata aŭ necerta. Kaj pri la origino certigas nur cifereca subskribo. Tial ekzemple programoj, kiuj instaliĝas en ret-krozilo, estas subskribitaj. Oni instalu ilin nur, se oni fidas la subskribinton. Se poste tamen montriĝas, ke estis (intenca) malicaĵo en la programo, eble oni povas akuzi lin por ricevi kompenson de la malutilo.
Se ret-mesaĝo estas ciferece subskribita, oni povas esti certe pri la identeco de la sendinto kaj (normale) pri la ne-maliceco de la dokumentoj, kiujn li sendis. Tio estas grava rimedo por kontraŭbatali virusojn. Sed ankoraŭ ne multaj uzas ciferecan subskribon kun siaj ret-mesaĝoj, kaj retpoŝtiloj normale bezonas aldonan programon por kontroli ciferecajn subskribojn.
Ni jam priskribis, kiel eblas uzi la publikan ŝlosilon de alia homo por sendi al li ĉifritan mesaĝon, kiun nur li povas legi (normale oni uzas du-ŝtupan metodon kun generita simetria ŝlosilo). Atentindas, ke ankaŭ la sendanto ne povas legi la mesaĝon, nek eventualan kopion, kiun li konservis. Se li volas konservi kopion, li devas kopii la tekston antaŭ la ĉifrado kaj eble ĉifri la kopion per sia propra publika ŝlosilo por malhelpi, ke tria persono legu ĝin.
Sendante mesaĝon al pluraj personoj necesas aparte ĉifri ĝin per ĉies publika ŝlosilo.
Senkomplike eblas kombini ĉifradon kun cifereca subskribo. Eblas apliki la subskribon antaŭ aŭ post la ĉifrado. Se oni subskribas antaŭ la ĉifrado, spionanto eĉ ne povas rimarki, ke iu kaj kiu subskribis.
Sendante subskribitan mesaĝon oni aldonu sian certigilon; tio ŝparas al la ricevanto la penon akiri ĝin de alie.
Indas ripeti, ke la kalkulado necesa por ĉifri kaj subskribi tute ne estus farebla sen komputilo. Tial estas klare, ke la komputilo helpu ankaŭ ĉe la administrado de ŝlosiloj kaj, ekzemple, (duon)aŭtomate havigu bezonatajn ŝlosilojn. Atentindas, ke necesas regula kontrolo de tiucele uzata komputilo, por certigi, ke la retpoŝta programaro ne estis malice modifita por, ekzemple,
Tiaj kontroloj estas analogaj al la kontroloj pri virusaj atakoj.
Uzantoj de simetriaj ĉifroj havas la problemon, kiel sekure interŝanĝi la ŝlosilon. Ni vidis, ke malsimetriaj ĉifroj kaj publikaj ŝlosiloj principe solvas tiun problemon: Oni simple publikigas sian publikan ŝlosilon, kiu evidente ne estas konfidenca.
Sed en TTT oni ofte uzas ĉifritan konekton, kvankam la uzanto ne posedas privatan ŝlosilon kaj la ret-servilo ne havis okazon sekrete sendi al la uzanto ŝlosilon. Kiel tio funkcias? Kiel uzanto (krozilo) kaj servilo ekhavas komunan kaj tamen sekretan ŝlosilon?
Por kompreni tion ni imagu, ke iu persono A volas sendi al persono B konfidencan valizon per nesekura transport-servo. A tial ŝlosas la valizon per seruro, kies (materian, eble metalan) ŝlosilon posedas nur li. Se ankaŭ B posedus identan ŝlosilon, la problemo estus solvita: B povus malfermi la valizon. Sed li ne havas la necesan ŝlosilon.
Tial B, ricevinta la valizon, almetas duan seruron, kies ŝlosilon li posedas, kaj resendas la valizon al A. A malfermas sian propran seruron kaj resendas la valizon (ankoraŭ protektatan per la seruro de B) al B. Tiu nun povas finfine depreni sian propran seruron kaj malfermi la valizon.
Dum la tuta transportado la valizo ĉiam estis protektita de seruro, kvankam A kaj B ne havis komunan ŝlosilon.
La malforta punkto de la procedo estas la identigo de la seruro de B. A devas esti certa, ke la seruro ĉe la revenanta valizo venas de B kaj ne de iu alia. B do devas iel aŭtentikigi la seruron.
Kiel eblas transformi tiun metodon al ĉifroj kaj ne-materiaj ŝlosiloj? Necesas havi ĉifrojn, kiuj estas komutecaj, t. e. ĉe kiuj estas egale, kiun el du ĉifroj oni aplikas unue kaj kiun poste. Multaj ĉifroj posedas tiun econ.
Same kiel en la ekzemplo de la valizo A kaj B bezonas po ĉifron, ni nomu ilin cA kaj cB, kun malĉifraj funkcioj dA kaj dB. A nun prenas mesaĝon m, ĉifras ĝin per cA kaj sendas la rezulton al B:
| cA (m) |
Tiu ĉifras per cB kaj resendas la rezulton:
| cB(cA (m)) |
A malĉifras per dA kaj resendas la rezulton; ĉar la ĉifroj estas komutecaj, la rezulto estas la sama, kvazaŭ nur B estus ĉifrinta ĝin:
| dA( cB( cA( m ))) = |
| cB( dA( cA( m ))) = |
| cB(m) |
Tion B povas malĉifri per dB. A kaj B konfidence interŝanĝis mesaĝon sen komuna ŝlosilo kaj sen malsimetriaj ĉifroj.
Por TTT-dialogoj, kie ekzemple aĉetantoj sendas sian kreditkartan numeron tra la Interreto, tiu metodo estas tre taŭga. A estas la TTT-servilo kaj B la TTT-uzanto, kaj tute ne necesas, ke B komence legitimu (aŭtentikigu) sin al A, ĉar la informoj de ret-servilo ja normale estas publikaj kaj alireblaj al ĉiu ajn. Gravas nur, ke la informoj senditaj de B kaj la respondoj de la servilo restu konfidencaj, kaj ke la servilo pruvu al la uzanto sian identecon. Tion ĝi faras per certigilo, por kiu ja necesas cifereca subskribo kaj do malsimetria ĉifro.
La priskribita metodo por konfidence interŝanĝi informojn per la TTT-protokolo HTTP nomiĝas "HTTPS" ("S" kiel "sekura").
En certaj situacioj necesas aŭtentikigi ne mesaĝon, sed sian propran identecon, ekzemple por eniri iun landon, domon aŭ gardatan areon. Tio eblas per ico-karto kun privata ŝlosilo, ĉar nur la posedanto scias (sciu) la PIN-on por funkciigi la karton.
Ne sufiĉas prezenti iun subskribitan mesaĝon (ekz. "mi estas XY"), ĉar tiun mesaĝon ja iu povus kopii kaj mem uzi kiel legitimilon. Necesas, ke la persono, al kiu oni volas legitimi sin, prezentu "mesaĝon", kiun oni subskribas. Tiu metodo nomiĝas "defio kaj respondo" (angle: challenge and response); la prezentado de la subskribenda mesaĝo estas kvazaŭ defio, kiun oni respondas per subskribo.
Estus malprudente, se la defio estus tute libere elektebla; la defianto ja povus peti subskribon al ĉeko aŭ mon-ĝirilo. Aliflanke ni vidis, ke devas esti arbitra elemento en la mesaĝo. Ekzemple oni povus uzi la titolon "sin-aŭtentikigo" kaj aldoni la aktualan tempon (kiun pli-malpli elektas la defianto) kaj hazardan nombron (kiun libere elektas la defianto, eble per komputila programo).
Se iu persono A laŭ la ĵus priskribita metodo legitimis sin al alia persono B, B povas prezenti la subskribitan mesaĝon al iu tria persono kaj tiel pruvi, ke A legitimis sin al li. Se tio ne estas dezirata, necesas alia metodo (vidu malsupre).
Ĝenerale estas dezirinde, ke aŭtentikigo estas pruvebla al triaj personoj, ĉar oni ofte bezonas triajn personojn (ekzemple tribunalon) por eldevigi siajn rajtojn, kiujn oni posedas pro alies subskribita mesaĝo. Se, ekzemple, komercisto havas subskribitan mendon de kliento, kiu subite malagnoskas (dementas) tiun mendon, estas esence, ke la komercisto povas pruvi al tribunalo, ke la kliento subskribis la mendon. Kiel ni vidis, tio eblas nur danke al malsimetriaj ĉifroj kaj publikaj ŝlosiloj.
Eĉ se oni tre zorge traktas sian privatan ŝlosilon (ico-karton, ĝian PIN-on), povas okazi, ke la ŝlosilo malsekretiĝas (estas perfidita). Ekstrema-okaze ja povus esti, ke iu perforte rabas ico-karton kaj per minacoj akiras la PIN-on.
En tia okazo necesas revoki la privatan ŝlosilon en la karto, ĉar subskriboj faritaj per ĝi ne (certe) venus de la laŭjura posedanto. Tia revoko okazas per publika anonco; precipe necesas informi sian certigan aŭtoritaton, ĉe kiu aliaj personoj povas demandi pri la orda stato de la ŝlosilo.
Bedaŭrinde subskribita mesaĝo ne diras, je kiu tempo ĝi estis subskribita, kaj se ĝi dirus, la tempo povus esti falsa. Tial revoko de ŝlosilo nuligas ĉiujn subskribojn iam ajn faritajn per tiu ŝlosilo. Oni ja ne scias, ĉu iu subskribo okazis antaŭ aŭ post la revoko.
El la ĵus priskribita scenaro oni vidas, ke ĉiu ajn subskribo estas daŭre en danĝero iĝi malvalida pro revoko de la ŝlosilo. Kontraŭ tiu danĝero ekzistas nur unu protekto: Necesas akiri subskribitan konfirmon de alia persono, kiu konfirmas, ke la mesaĝo kun la originala subskribo ekzistis je iu certa tempo. Se la ŝlosilo estas revokita poste, la subskribo tamen restas valida. La procezo do povus esti jena:
| tempo T1 | A subskribas mesaĝon al B. |
| tempo T2 | B ricevas la mesaĝon de A. |
| tempo T3 | B akiras konfirmon subskribitan de C, ke la mesaĝo kun la subskribo de A ekzistas. |
| tempo T4 | A revokas sian ŝlosilon. |
| tempo T5 | B povas pruvi, ke la mesaĝo estis subskribita antaŭ T3, do antaŭ la revoko, do la subskribo validas. |
Tian konfirmon ordinare donas iuj ĝenerale fidindaj instancoj, ekzemple certigaj aŭtoritatoj, aŭ ekzemple notarioj. Por tre gravaj dokumentoj estas tre konsilinde, akiri notarian konfirmon laŭeble frue.
Ni vidis, ke per publikaj ŝlosiloj eblas pagi ciferece, per ciferece subskribitaj mon-ĝiroj. Por multaj negocoj tio sufiĉas. Kelkfoje oni tamen deziras pagi anonime, kaj tio ne eblas per ĝiro, kiu devas ja indiki, de kies konto oni prenu la monon.
Por anonima pagado necesas kontanta mono. Ĝia realigo prezentas du problemojn:
La problemoj estas solveblaj. Por kompreni tion ni konsideru iom strangan landon, kie la centra banko presas monbiletojn sen numeroj sur paperon, kiun rajtas provizi ĝiaj klientoj. La kialo estas, ke la banko povus registri la fibro-strukturon de la papero por poste rekoni la monbiletojn kaj tiel scii, kiu elspezis ilin.
Eĉ se la paperon provizas la klientoj, la banko povus tamen registri la fibro-strukturon. Sed la klientoj metas sian paperon en fermitan koverton, kune kun karbo-papero, kaj la banko stampas tiun koverton tiel, ke la bildo de la monbileto aperas tra la karbo-papero sur la papero. Tiel la kliento ekhavas sian monbileton, la banko scias lian identecon por depreni la valoron de lia konto, sed ĝi tamen neniam vidis la paperon.
Tiu stranga banko malstrangiĝas, kiam temas pri cifereca mono. Monbiletoj (aŭ moneroj) tie estas (grandaj) nombroj signitaj per speciala privata "mon-ŝlosilo" de la banko. Prezentante tian nombron al la banko oni rericevas la valoron.
Por ke la banko ne registru, al kiu ĝi signis kiun nombron, la kliento prezentas la nombron en ĉifrita formo. Post ricevo de la subskribo li malĉifras la nombron kaj la subskribon (necesas ĉifro, kiu ne influas la validecon de la subskribo). Nun la kliento havas "monbileton", kiun la banko ne konas, sed kiu tamen estas valida.
Restas la problemo, ke la kliento povus kopii la monbileton kaj elspezi ĝin plurfoje. Por eviti tion oni postulas, ke la kliento metu en la "monbileton" sian nomon (identecon) en ĉifrita formo. Ĉe la elspezo la akceptanto de la bileto postulas, ke la paganto malĉifru parton de la identeco; se li du- aŭ plurfoje pagas, li riskas, ke la tuta identeco malkaŝiĝu.
La disvastiĝo de altkvalitaj koloraj kopiiloj kaj presiloj minacas la tradician, paperan monon, ĉar falsistoj nun disponas pri bona ilaro. Valutaj bankoj kontraŭbatalas tiun problemon per speciala papero, plastaj monbiletoj kun "fenestroj", spegulecaj markoj, hologramoj ktp. Sed ekzistas ankaŭ kriptografia solvo de la problemo.
Tiu solvo baziĝas sur la fakto, ke eblas meti fluoreskantajn (lumantajn) fibrojn en la monbiletan paperon, sed ne precize antaŭfiksi ilian lokon. Post la produktado de la papero eblas mezuri la lokon de tiaj fibroj kaj ciferece subskribi iliajn koordinatojn per privata "mon-ŝlosilo"; la rezulton oni presus sur la bileton. Por kontroli la aŭtentikecon de bileto oni denove mezurus la koordinatojn de la fibroj kaj tiam kontrolus la subskribon.
Falsanto, kiu simple kopias monbileton sur alian paperon, ne povus kopii la precizan situon de la fluoreskantaj fibroj.
Ni vidis supre, ke per sia privata ŝlosilo oni povas pruvi sian identecon, sen malkaŝi la ŝlosilon. Ni vidis ankaŭ, ke tiu sin-legitimado estas pruvebla al aliaj; la persono, al kiu oni aŭtentikigis sin, povas pruvi tion al triaj personoj.
En certaj situacioj tio ne estas dezirinda. Eble iu persono estas membro en iu asocio, sed ne volas, ke tiu fakto estu ĝenerale konata. Se li devas legitimi sin por partopreni en kunveno de la asocio, iu povus per la legitimado pruvi la membrecon.
Ekzistas metodoj de sin-legitimado (identec-pruvo), kiuj ne donas al observanto ian scion pri la uzataj sekretoj. Ili tial nomiĝas nul-sciaj metodoj (angle: zero-knowledge). La principo estas bone demonstrebla per jena scenaro:
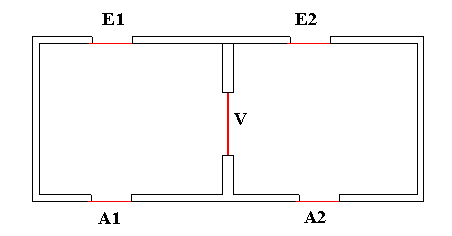
En iu domo estas du ĉambroj kun pordo V inter ili, kiu havas sekretan seruron. Krome ĉiu ĉambro havas nur-eniran pordon (E1, E2) kaj nur-eliran pordon (A1, A2):

Iu persono A posedas la sekreton por malfermi la pordon. Tiam A povas jene pruvi al B, ke li scias la sekreton:
| B restas antaŭ la domo, A elektas unu el la pordoj E1 aŭ E2 kaj eniras la domon. |
| B de ekstere certiĝas, ke E1 kaj E2 estas fermitaj. |
| B vokas al A, el kiu el la pordoj A1 aŭ A2 li venu. |
| Se A hazarde estas en la ĝusta ĉambro, li simple eliras. Alie li devas malfermi la sekretan seruron kaj eliri. Ĉiuokaze li povas veni el la postulita pordo. Alia persono, kiu ne scias la sekreton, povus fari tion nur en 50 % de la provoj. |
| Se A sufiĉe ofte (10, 20, 50 fojojn) sukcesis, B kredas, ke A posedas la sekreton. |
Ĉu B povus pruvi al iu tria persono C, ke A legitimis sin? Li povus registri ĉion sur video-bendo; sed li ne povus pruvi, ke li ne antaŭe interkonsentis kun la persono tie videbla, kiam li postulos kiun pordon. Do la videoaĵo pruvas nenion.
La matematika analogiaĵo de la "sekreta pordo" povas esti la radiko de iu nombro N en speciala (modula) aritmetiko, en kiu radikoj estas malfacile kalkuleblaj. La procedo de la pruvado estas jena:
| A elektas iun nombron m kaj diras al B la nombron M=m2 aŭ la nombron M=m2·N. |
| B decidas, ĉu li petu de A la radikon de m aŭ de (m·N). |
| Se A scias la radikon de N, li povas kalkuli ambaŭ nombrojn. Se li ne scias la radikon, li povas kalkuli nur unu, depende de sia elekto en la unua paŝo. |
Ankaŭ ĉe tiu procedo A povas ĉiam plenumi la postulon de B, se li antaŭe scias, kion B postulos.