Enkonduko en la aŭtomatan daten-prilaboradon (2)

1 Hierarkiaj strukturoj

1.1 Hierarkioj kaj arboj

En la unua parto de la kurso "Enkonduko al la aŭtomata daten-prilaborado" (leciono 11) ni konatiĝis kun dosieraj sistemoj. Tiaj dosieraj sistemoj tre ofte estas aranĝitaj en hierarkio, kiu konsistas el du specoj de objektoj:

simplaj dosieroj, kiuj enhavas datenojn
dosierujoj, kiuj enhavas dosierojn kaj aliajn dosierujojn

La fakto, ke dosierujo povas enhavi pliajn dosierujojn, ebligas la konstruadon de grandaj hierarkiaj strukturoj, kies partoj estas konstruitaj same kiel la tuto (dosierujo en dosierujo en dosierujo…).

La vorto "hierarkia" signifas, ke la elementoj de la strukturoj estas sur pluraj ŝtupoj, kaj iuj elementoj estas "superaj" al aliaj. Ekzemple dosierujo estas supera al ĉiuj dosier(uj)oj, kiujn ĝi enhavas.

Hierarkioj ekzistas sur multaj kampoj. La malgranda ekzemplo el la antaŭa kurso eblas klarigi kelkajn aspektojn. Temas pri la (fantazia) hierarkio de dungitoj en entrepreno, prezentata en la formo de arbo, foje nomata struktur-bildo:

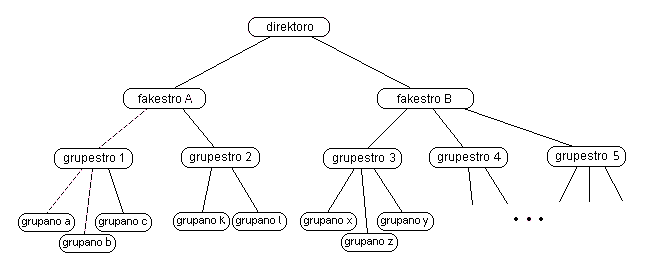
Oni rimarkas, ke en informadiko la arboj kreskas malsupren! Arbo estas ĝenerala formo por reprezenti hierarkion; oni povas diri, ke (en informadiko) arbo kaj hierarkio estas la sama afero: Ĉiuj hierarkioj estas reprezenteblaj kiel arboj, kaj ĉiuj arboj reprezentas hierarkion. La ekzempla stukturo montras kelkajn ĝeneralajn ecojn de hierarkioj:

Ekzistas precize unu elemento, kiu estas super ĉiuj aliaj (la direktoro). Tiu elemento nomiĝas la radiko de la arbo.
Ekzistas elementoj, sub kiuj estas aliaj elementoj (en la ekzemplo tio estas la "estroj" kaj la direktoro).
Ekzistas elementoj, sub kiuj ne estas aliaj elementoj (la grupanoj). En ĝeneralaj arboj ili nomiĝas folioj.
Ekzistas paroj de elementoj, en kiuj neniu estas super la alia (ekzemple "fakestro A" kaj "fakestro B", sed ankaŭ "fakestro A" kaj "grupestro 4 de fako B").
De ĉiu elemento estas precize unu vojo al la radiko. Ĉiuj partoj de tiu vojo iras "supren".
Inter po du elementoj estas precize unu vojo. Tiu vojo konsistas el du pecoj; la partoj de la unua peco iras "supren" kaj la partoj de la dua peco iras "malsupren". Unu el tiuj pecoj povas esti "malplena".

1.2 Rikuro

Ni vidis, ke la priskribo (aŭ difino) de dosierujoj mem uzis la vorton "dosierujo": Dosierujo povas enhavi dosierujojn. Tiaj strukturoj, kies partoj sekvas la samajn regulojn kiel la tuto, nomiĝas rikuraj. La priskribo de "dosierujo" estas rikura priskribo", ĉar ĝi mem uzas la (priskribatan) vorton "dosierujo".

Rikuro estas tre grava principo en informadiko, ĉar ĝi permesas redukti strukturojn al pli simplaj strukturoj. Se, ekzemple, oni diras, ke arbo konsistas el radiko, de kiu povas "dependi" aliaj arboj, oni difinis arbon per arboj, sed tiuj sub-arboj estas malpli grandaj, do pli simplaj.

Tiaj rikuraj difinoj utilas ĉe la prilaborado de strukturoj. Ekzemple oni povas utiligi la rikuran difinon de arbo por nombri la elementojn (verticojn) de arbo laŭ jenaj reguloj:

Se arbo konsistas nur el radiko, ĝi havas unu (1) verticon (ne-rikura regulo).
Alie necesas nombri la verticojn de ĉiuj sub-arboj, adicii la nombrojn kaj aldoni 1 por la radiko (rikura regulo).

Tiuj reguloj funkcias, ĉar la nombrataj arboj iĝas pli kaj pli malgrandaj; kiam oni alvenas ĉe la folioj, ili konsistas nur el unu vertico, kaj eblas apliki la unuan regulon. Ĉiu sistemo de reguloj bezonas almenaŭ unu ne-rikuran regulon; alie la rikuro ne povus finiĝi.

La principo de rikuro estas konata ankaŭ en matematiko, kiu difinas rikurajn funkciojn. Konata ekzemplo estas la faktorialo, funkcio ofte esprimata per krisigno (!) kaj neformale difinata per tri punktoj:

n! = 1 · 2 · 3 · … (n−1) · n

Oni facile kalkulas, ke 1!=1, 2!=2, 3!=6, 4!=24 ktp.; sed la tri punktoj ne estas ekzakta esprimilo. Rikura difino de la faktorialo estas jena:

La faktorialo de 1 estas 1.
Se n estas natura nombro, la faktorialo de (n+1) estas (n+1)·n!.

Specimenaj demandoj

Kio estas hierarkia strukturo?
Kiel interrilatas hierarkioj kaj arboj?
Kiel nomiĝas la plej supra elemento de arbo?
Kiuj elementoj estas la "folioj" de arbo?