

 Enkonduko en la aŭtomatan daten-prilaboradon (2)
Enkonduko en la aŭtomatan daten-prilaboradon (2)
Informo estas grava nocio en informadiko. Kiam oni esploras ĝin, montriĝas, ke hierarkioj estas bona helpilo por tio.
En la ĉiutaga vivo oni interrilatigas la nocion "informo" kun scio, sed ankaŭ kun signifo kaj interpreto. Tio malfaciligas ĝian formalan traktadon, ĉar interpretado kaj signifo estas io ekster la informo mem.
En informadiko informo rilatas al du gravaj aliaj nocioj: dateno kaj mesaĝo. Ĉar mesaĝo estas datenaro sendata de sendanto al ricevanto, tiuj du nocioj tre similas rilate la enhavatan informon. Por niaj nunaj konsideroj la nocio "mesaĝo" estas tre utila, ĉar la sendo de mesaĝo implicas, ke eblas havi aŭ ne havi certan informon. Unu el la celoj de informadiko estas mezuri la diferencon inter tiuj du statoj.
Al ĉiu, kiu klopodas parkerigi certan informon, estas evidente, ke informo estas kvanta afero: ekzistas mesaĝoj, kiuj bezonas pli da tempo por parkerigo ol aliaj. Same ekzistas mesaĝoj, kiuj sur papero, magnetdisko aŭ alia datenportilo bezonas pli da spaco ol aliaj.
Tiu kvanto aŭ grandeco (amplekso) de informo, kiun ni celas mezuri, estas ne la sama afero kiel la tuta informo; ĝi estas nur unu el ĝiaj ecoj. Ni nomas ĝin informacio. Informacio estas la mezurebla kvanto de la informenhavo de mesaĝo.
Informacio do tute ne koncernas interpreton, signifon ktp. Du pecoj de informo povas havi tute malsamajn temojn, ekzemple filozofian teorion kaj instrukciojn pri la uzo de malfermilo de ladskatoloj. Iliaj enhavoj do tute ne estas kompareblaj. Sed eblas decidi (mezuri), ĉu ilia informacio estas egala, aŭ ĉu la unua havas pli da informacio, aŭ ĉu la dua.
Kiel oni mezuru informon? Ekzistas diversaj ebloj, sed ili havas malavantaĝojn:
Meze de la 20-a jarcento parto el tiuj konsideroj estis konata, aliaj tute ne. Tamen Claude SHANNON (1916–2001) tiutempe kreis teorion por mezuri informacion, kiu validas ĝis nun. Laŭ li, la informacio de iu mesaĝo dependas ne nur de la mesaĝo mem, sed de la komunika procezo, kiu konsistas el sendanto, mesaĝo, kanalo (tra kiu oni sendas la mesaĝon) kaj ricevanto. Laŭ Shannon la informacio en mesaĝo dependas de du el tiuj elementoj: la mesaĝo mem kaj la ricevanto.
La teorio de Shannon mezuras informacion per la nombro de decidoj, kiuj necesas por eltrovi la informon. Tio similas al la societa ludo de "dudek demandoj", en kiu ludanto rajtas fari dudek demandojn respondeblajn per "jes" aŭ "ne" por eltrovi iun ajn personon aŭ objekton. Ĉe tio ili kreas hierarkion de objektoj, en kiu la demandoj estas la nodoj de la hierarkio.
| Konkretaĵoj | ||||
|---|---|---|---|---|
| vivaĵoj | nevivaĵoj | |||
| animaloj | plantoj | … | ||
| homoj | bestoj | florplantoj | senfloraj plantoj | |
Analoge al tiu ludo Shannon demandis, per kiom da jes-ne-demandoj eblas trovi la enhavon de iu teksto. Ĉar teksto konsistas el signoj, eblas redukti tion al la demando, per kiom da demandoj oni povas eltrovi iun signon en certa teksto. Trovante unu signon post alia oni povas eltrovi la tutan tekston.
Kiel ekzemplon ni konsideru signon el la alfabeto de Esperanto. Tiu alfabeto enhavas 28 literojn. Ni ignoru la diferencon inter majuskloj (A–Z) kaj minuskloj (a–z), la "usklecon", kaj koncentriĝu al la elekto inter "a", "b", … "z". Kiom da jes-ne-demandoj ni devas fari por eltrovi tian signon? Aŭ, kiom da ŝtupoj havas la hierarkio de la signoj?
Ni povus simple demandi "ĉu estas 'a'?", "ĉu estas 'b'?" kaj tiel plu, kaj plej malfrue post 27 demandoj ni scius la literon. Je bona ŝanco ĝi estas "a", tiel ke unu demando sufiĉas. Sed mezume ni verŝajne bezonas inter 10 kaj 15 demandojn. Ĉu eblas pli rapide?
Estas pli bone krei "ekvilibran hierarkion" da signoj, do dividi la alfabeton en du proksimume samgrandajn partojn kaj, ekzemple, unue demandi: "Ĉu la litero estas inter (inkluzive) 'a' kaj 'j'?" Tiel ni ne havas ŝancon eltrovi la ĝustas literon jam per la unua demando, sed ni certe duonigas la eblan signaron. Kaj pri tiu resto ni povas procedi same: Se la unua respondo estas "ne", la signo devas esti inter 'k' kaj 'z', kaj la dua demando povas esti: "Ĉu la litero estas inter 'k' kaj 'r'?" Se la demando estas "jes", per tria demando eblas trovi, ĉu la signo estas inter 'k' kaj 'n' ktp. Fine ni eble trovas, ke la signo estas "t", kaj ni bezonis kvin demandojn, laŭ la sekva tabelo ("jes" signifas ĉiam, ke la signo estas en la maldekstra parto):
| a – ĵ | k – z | ne | ||||||||||||||||||||||||||
| a – f | g – ĵ | k – r | s – z | ne | ||||||||||||||||||||||||
| a – ĉ | d – f | g – ĥ | j – ĵ | k – n | o – r | s – u | ŭ – z | jes | ||||||||||||||||||||
| a b | c ĉ | d e | f | g ĝ | h ĥ | i j | ĵ | k l | m n | o p | r | s ŝ | t u | ŭ v | z | ne | ||||||||||||
| a | b | c | ĉ | d | e | f | g | ĝ | h | ģ | i | j | ĵ | k | l | m | n | o | p | r | s | ŝ | t | u | ŭ | v | z | jes |
| t | ||||||||||||||||||||||||||||
Ni do povas diri, ke la respondaro "ne-ne-jes-ne-jes" identigas literon "t". Per kvin demandoj eblas eltrovi ĉiun Esperanto-literon. Kelkajn eblas eltrovi jam per kvar demandoj.
Laŭ propono de Shannon tia jes-ne-demando nomiĝas "bito". Nia unua mensa eksperimento montris, ke Esperanto-litero havas informacion de maksimume 5 bitoj, eble malpli.
Tiu metodo donas al ni duuman kodon por ĉiu litero, se ni metas "0" por "jes" kaj "1" por "ne":
| A | 00000 |
| B | 00001 |
| C | 00010 |
| Ĉ | 00011 |
| D | 00100 |
| E | 00101 |
| F | 0011 |
| … | |
| S | 11010 |
Per la jes-ne-demandoj ni faris gravan paŝon al la preciza mezurado de informacio. Sed la procedo, ĉiam dividi la eblajn signojn en du samgrandajn partojn, ne estas optimuma. Ĉiu parolanto de Esperanto scias, ke la literoj "a", "e", "o" kaj "s" estas tre oftaj, kaj ke la literoj "h" kaj "ĥ" estas maloftaj. Se, ekzemple, oni reduktis la eblajn signojn al {d, e, f}, ne estas prudente demandi, ĉu la signo estas "d"; ofte la respondo estas "ne", kaj necesas fari plian demandon por diferencigi inter "e" kaj "f". Prefere oni demandu, ĉu la signo estas "e", kaj ofte la respondo estos "jes", tiel ke ne necesas plia demando.
El tio ni lernas, ke utilas unue/ofte demandi pri "oftaj" signoj. La matematiko uzas anstataŭ "ofta" la esprimon "probabla". La probableco de iu signo s estas ĝia mezuma ofteco, alivorte: la "ŝanco", ke ĝi aperas.
Kredeble pri ĉiuj alfabet-skribaj lingvoj ekzistas statistikoj pri la ofteco de literoj. Iliaj rezultoj dependas de la speco de analizitaj tekstoj. Pri Esperanto ekzistas pluraj statistikoj. Pejno-Simono (Simon Payne) analizis tekstojn kun 355.381 vortoj kaj ricevis jenan rezulton (vidu http://ourworld.compuserve.com/homepages/profcon/esperant.htm):
| Tabelo 1: Oftecoj en elcentoj laŭ Pejno-Simono | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Saksia Esperanto-Junularo analizis "La Senĉesa Rakonto", kun iom pli ol 100.000 signoj. Jen la rezultoj (vidu http://www.uni-leipzig.de/esperanto/material/material.html#literofteco):
| Tabelo 2: Oftecoj laŭ Saksia Esperanto-Junularo | ||||||
|---|---|---|---|---|---|---|
| litero | ĉapitroj | sumo | ofteco | |||
| 0 | 1, 2 | 3–5 | /100.000 | /100 | ||
| a | 2040 | 4901 | 5583 | 12524 | 11852 | 11,852 |
| i | 1970 | 4240 | 5268 | 11478 | 10862 | 10,862 |
| e | 1550 | 3567 | 4167 | 9284 | 8786 | 8,786 |
| n | 1397 | 3089 | 3691 | 8177 | 7738 | 7,738 |
| o | 1440 | 3066 | 3650 | 8156 | 7718 | 7,718 |
| s | 1226 | 2750 | 3386 | 7362 | 6967 | 6,967 |
| l | 1212 | 2452 | 2939 | 6603 | 6249 | 6,249 |
| r | 1029 | 2291 | 2845 | 6165 | 5834 | 5,834 |
| t | 1000 | 2281 | 2710 | 5991 | 5670 | 5,670 |
| k | 781 | 1792 | 1902 | 4475 | 4235 | 4,235 |
| u | 566 | 1415 | 1722 | 3703 | 3504 | 3,504 |
| j | 629 | 1417 | 1466 | 3512 | 3324 | 3,324 |
| m | 558 | 1186 | 1440 | 3184 | 3013 | 3,013 |
| d | 477 | 1008 | 1343 | 2828 | 2676 | 2,676 |
| p | 434 | 921 | 1170 | 2525 | 2390 | 2,390 |
| v | 318 | 699 | 963 | 1980 | 1874 | 1,874 |
| g | 172 | 562 | 578 | 1312 | 1242 | 1,242 |
| b | 238 | 386 | 421 | 1045 | 989 | 0,989 |
| f | 177 | 412 | 424 | 1013 | 959 | 0,959 |
| ĉ | 123 | 336 | 369 | 828 | 784 | 0,784 |
| ĝ | 92 | 296 | 386 | 774 | 732 | 0,732 |
| ŭ | 111 | 297 | 328 | 736 | 697 | 0,697 |
| c | 88 | 299 | 258 | 645 | 610 | 0,610 |
| z | 74 | 203 | 211 | 488 | 462 | 0,462 |
| ŝ | 71 | 140 | 164 | 375 | 355 | 0,355 |
| h | 54 | 180 | 122 | 356 | 337 | 0,337 |
| ĵ | 21 | 52 | 60 | 133 | 126 | 0,126 |
| ĥ | 0 | 6 | 12 | 18 | 17 | 0,017 |
sumo| 17848 |
40244 |
47578 |
105670 |
100002 |
100,002 |
|
Kion signifas tiuj malsamaj oftecoj? Tion oni komprenas, se oni rigardas du ekzemplojn de parte konataj vortoj:
| unua nekonata vorto: | k | s | ||||
| dua nekonata vorto: | k | ŭ |
La unua vorto povus esti "kantas", "krevas", "kultas", "klinas", "klaĉas", "kurbas", ktp., kaj krome ĝi povus esti la "-is"-, "-os"- aŭ "-us"-formo de tiuj vortoj. Sed la dua vorto povas esti nur "kvazaŭ". La malofta litero "ŭ" do donas al ni multe pli da informacio ol la ofta litero "s" (kiu estas ofta precipe ĉe vortofino).
Matematike oni nomas la mezan oftecon de signo ĝia probablo. La teorio de Shannon difinas, ke la informacio en iu signo s egalas al la duuma logaritmo de la inverso de ĝia probablo p(s):
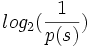
La duuma logaritmo log2 de iu nombro diras, kiom ofte ĝi enhavas la faktoron 2, ekzemple:
| 32 = 2·2·2·2·2, do la duuma logaritmo de 32 estas 5. |
| 16 = 2·2·2·2, do la duuma logaritmo de 16 estas 4. |
| 8 = 2·2·2, do la duuma logaritmo de 8 estas 3. |
| 4 = 2·2, do la duuma logaritmo de 4 estas 2. |
| 2 = 2, do la duuma logaritmo de 2 estas 1. |
| la duuma logaritmo de 1 estas 0. |
La matematiko difinas la logaritman funkcion ankaŭ por ne-entjeraj valoroj. Por kelkaj literoj de tabelo 1 ni trovas jenajn informaciojn laŭ Shannon:
| litero | ofteco | inversa ofteco | informacio |
|---|---|---|---|
| A | 0,1208 | 8,278 | 3,049 |
| O | 0,0990 | 10,101 | 3,336 |
| E | 0,0963 | 10,384 | 3,376 |
| U | 0,0331 | 30,21 | 4,917 |
| C | 0,0100 | 100,0 | 6,644 |
| Ŭ | 0,0051 | 196 | 7,615 |
| Ĥ | 0,0002 | 5000 | 12,3 |
Tiel ni scias la informaciojn de la diversaj literoj kaj povas nun kalkuli, kiom da informacio meze havas unu litero. La probablo diras al ni, kiom ofte (mezume) aperas la diversaj literoj. Kompreneble la pli oftaj literoj pli forte kontribuas al la meza informacio; necesas multipliki la informaciojn de la signoj per iliaj probabloj:
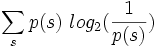
Tio estas bela difino, kies valoroj ŝajnas intuicie akcepteblaj, sed kiu estas ĝia praktika signifo? Ni rigardu fantaziajn alfabetojn, en kiuj ĉiuj literoj estas egale oftaj. Ekzemple jen estas la "alfabeto" de la 4 lud-kartaj emblemoj:
| probablo | informacio | ||
|---|---|---|---|
| ♣ | trefo | 0,25 | 2 |
| ♠ | piko | 0,25 | 2 |
| ♥ | kero | 0,25 | 2 |
| ♦ | karoo | 0,25 | 2 |
Efektive la informacio "2", kiu rezultas por la signoj de tiu alfabeto, egalas al la nombro de jes-ne-demandoj (bitoj), kiuj necesas por decidi inter kvar simboloj. La difino per la logaritmo do ŝajnas havi rilaton al la difino per jes-ne-demandoj. Tio validas ankaŭ por alfabetoj kun 8, 16, 32… literoj, kies simboloj havas informacion de 3, 4, 5… bitoj.
Sed kiu estas la signifo por alfabetoj kun malegalaj oftecoj? Ilin necesas kodi tiel, ke la oftaj simboloj havas mallongajn kodojn kaj la maloftaj simboloj havas longajn kodojn. Pli precize, la longo de la kodo estu simila (laŭeble egala) al la informacio de la simbolo. Eksperimente ni reduktu la Esperanto-alfabeton al la kvar literoj A, K, R kaj U, kun jenaj oftecoj (tiom grandigitaj, ke la sumo estu 1):
| litero | ofteco | inversa ofteco | informacio |
|---|---|---|---|
| A | 0,4803 | 2,082 | 1,058 |
| K | 0,1535 | 6,515 | 2,704 |
| R | 0,2346 | 4,263 | 2,092 |
| U | 0,1316 | 7,598 | 2,926 |
Laŭ la informacio litero A havu kodon el 1 bito, R el 2 bitoj kaj K kaj U el po 3 bitoj. Ĉu tia kodo ekzistas? Jes, ekzemple oni jene aranĝu la jes-ne-tabelon:
| tiel, ke rezultas jenaj kodoj: |
| ||||||||||||||||||||||||
Tiaj kodoj estas praktike utilaj, ĉar ili bezonas mezume malpli da bitoj ol aliaj kodoj. Ili do permesas, en la sama tempo transsendi pli la signoj. Tamen ilia graveco malkreskis, ĉar nun ekzistas algoritmoj por densigi datenojn, kiuj ne bezonas antaŭscion pri la probableco de la signoj. Tiaj algoritmoj trovas kodon, kiu estas bona por la densigataj datenoj, kaj storas tiun kodon en la densigita informo.
Se en optimuma kodo la longoj de la kod-valoroj estu egala al la informacio de la signoj, kion tio signifas por kodoj, kie ĉiuj kod-valoroj estas egale longaj (ekz. en Askio)? Ili estas optimumaj nur tiam, se ĉiuj signoj estas egale probablaj (oftaj). Ekzemple kodo kun 7 bitoj estas optimuma por 128 signoj, kiuj havas egalan probablon de 1/128 (= 0,78125 %); kodo kun 4 bitoj estas optimuma por 16 signoj, kiuj havas egalan probablon de 1/16 (= 6,25 %).
Ni vidis, ke la saman informon oni povas kodi diversmaniere, kaj ke la rezultoj povas havi malsamajn longojn. Se la kodaĵo estas pli longa ol necesa, oni diras, ke la kodo estas redunda. La rilato de la nenecesa informo al la tuta estas la redundo de la kodo.
Multaj kodoj estas redundaj. Ekzemple por kodi tekstojn estas praktike, se ĉiuj signoj havas kodojn de la sama longo (7 bitoj en Askio). Ĉar la signoj ne estas egale probablaj, tia kodo nepre estas redunda.
Laŭ la supra tabelo "Oftecoj laŭ Saksia Esperanto-Junularo" eblas kalkuli, ke signo en la analizita teksto portas mezume 4,15 bitojn da informacio. Lingvo, kiu egale ofte (egale probable) uzus la 28 literojn de la alfabeto, povus per ili kodi mezume 4,81 bitojn, do 0,66 bitojn pli. Skribita Esperanto do havas redundon de almenaŭ 0,66/4,81, aŭ preskaŭ 14 procentoj.
La vera redundo estas pli granda, ĉar ni ankoraŭ ne konsideris la fakton, ke la ofteco de literoj dependas de ilia kunteksto. Ekzemple estas tre malprobable, ke post litero "c" sekvu litero "s"; multe pli probable sekvas vokalo. Se oni konsideras la probablojn por litero-duoj, -trioj kaj tiel plu, oni vidas, ke la redunco de la lingvo estas konsiderinda. Eblas kalkuli, ke unu litero en normala teksto portas nur ĉirkaŭ unu biton; la redundo do estas 3,81/4,81 aŭ 79 procentoj. En certaj situacioj la redundo estas eĉ pli alta, ekzemple kiam homo diras "bonan tagon".
La programo gzip densigas datenojn laŭ la priskribita principo: Ĝi trovas bonan kodon, aplikas ĝin kaj storas la kodon kune kun la densigita informo (iusence eĉ en ĝi). Jen kelkaj ekzemploj, kiel gzip densigas. Ni uzas du specojn de datenoj:
| Leciona teksto | Ciferoj 123456789 | |||
|---|---|---|---|---|
| Enigitaj signoj | Densigitaj signoj | Densigo | Densigitaj signoj | Densigo |
| 10 | 30 | 300 % | 30 | 300 % |
| 20 | 40 | 200 % | 32 | 160 % |
| 30 | 50 | 167 % | 33 | 110 % |
| 40 | 60 | 150 % | 33 | 82,5 % |
| 50 | 68 | 136 % | 33 | 66,0 % |
| 100 | 107 | 107 % | 33 | 33,0 % |
| 1.000 | 443 | 44,3 % | 39 | 3,9 % |
| 10.000 | 3255 | 32,6 % | 66 | 0,66 % |
| 20.000 | 5618 | 28,1 % | 85 | 0,43 % |
Oni konstatas plurajn ecojn: