

 Enkonduko en la aŭtomatan daten-prilaboradon (2)
Enkonduko en la aŭtomatan daten-prilaboradon (2)
Hierarkioj ofte ekestas per tio, ke oni dispartigas grandan problemon al malgrandaj problemoj. Bela ekzemplo pri tio estas la tasko de la "Turoj de Hanojo": Necesas transporti turon el diskoj de unu loko al alia.
La ludon verŝajne inventis la franca matematikisto Edouard LUCAS (1842–1891) en la jaro 1883. Por ke la ludo ne aspektu infana, li transmetis ĝin en orientan monaĥejon, kie monaĥoj devas transporti turon el 64 diskoj. (Kiam ili fintransportis ĝin, la mondo finiĝos.) Ĉar Hanojo situas (de Eŭropo) en oriento, la ludo ricevis la nomon "Turoj de Hanojo".
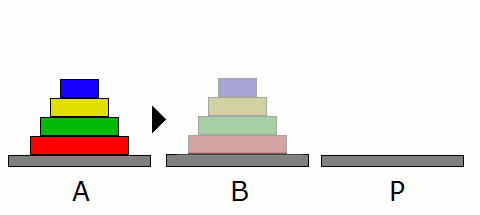
La turo konsistas el diskoj malsame grandaj, kaj maldikiĝas supren, do ĉiu disko kuŝas sur pli granda disko (aŭ sur la grundo). Tiel devas resti dum la tuta transportado, kaj ekzistas nur unu libera loko ("parkejo"), kie eblas lasi diskon (aŭ turon). Ni diru, ke la turo staras en loko A, devas esti transportita al loko B, kaj la parkejo estu P. Eblas transporti nur unu diskon samtempe.
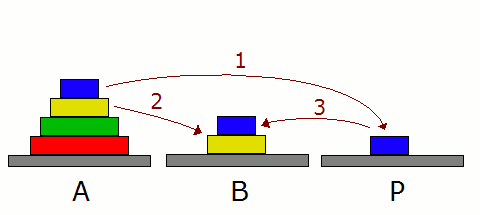
Komence kaj fine de la ludo ekzistas nur unu turo, sed dum la ludo povas ekzisti du aŭ tri. Tial la ludo en kelkaj lingvoj nomiĝas "Turo de Hanojo", en aliaj "Turoj de Hanojo".
Ni konsideru kelkajn simplajn kazojn kun malmultaj diskoj:
En Vikipedio ekzistas artikolo pri la Turoj de Hanojo, kiu prezentas la kazojn de 3 aŭ 4 diskoj per vivaj bildetoj.
Videblas, ke ju pli altas la turo, des pli komplika la tasko estas (kaj des pli da movoj necesas). Sed estas facile dispartigi la taskon: Por movi turon el N diskoj oni
Tiel ni reduktis la taskon, transporti turon el N diskoj, al la dufoja transportado de turo kun N−1 diskoj. Eblas pensi, ke ekzistas pli rapida metodo, sed detala analizo montras, ke ne. Jena tabelo skizas ekzemplon kun 3 diskoj:
| transportu 3 diskojn de A al B | ||||||
|---|---|---|---|---|---|---|
| transportu 2 diskojn de A al P | transportu diskon "3" de A al B | transportu 2 diskojn de P al B | ||||
| transportu diskon "1" de A al B | transportu diskon "2" de A al P | transportu diskon "1" de B al P | transportu diskon "1" de P al A | transportu diskon "2" de P al B | transportu diskon "1" de A al B | |
Laŭ tiu dispartigo oni en ĉiu ŝtupo povas koncentriĝi al la supre donitaj subtaskoj 1, 2 kaj 3. La reguloj por la subtaskoj 1 kaj 3 estas rikuraj, ĉar ili parolas pri la movado de (malpli altaj) turoj. Regulo 2 ne estas rikura; ĝiparolas nur pri la movado de disko (elementa tasko, ne plu dividebla).
Se oni prezentas la tabelon kiel arbon, ĉiu "tur-mova" vertico havas tri sub-verticojn: du el ili estas denove tur-movaj, kaj la meza estas disko-mova kaj ne havas sub-verticojn.
Kiel do la rikuro finiĝas? En nia regulo kun la tri sub-taksoj ni forgesis ion: ĝi validas nur por turoj kun minimume du diskoj. Por movi turon el unu disko oni simple movas tiun diskon. Tiumaniere la rikuro ne estas senfina.
La subdivido de la problemo donis al ni ne nur regulojn, kiel procedi. Ĝi ankaŭ igis la problemon pli facile superrigardebla kaj tiel solvas du gravajn sub-problemojn:
Nia dispartigo diras al ni, kiel ni procedu por transporti la turon, sed povus esti, ke tio kontraŭas la kernan regulon de la ludo: Disko ne povas kuŝi sur malpli granda disko. Sed analizo de nia subdivido montras, ke tio ne povas okazi:
Se ni komence metas la unuan diskon sur la malĝustan lokon, ankaŭ la fina turo estos sur la malĝusta loko. Ĉar ekzistas nur du lokoj (krom A), nome B kaj P, principe ekzistas du ebloj: La fina turo staros sur la sama loko kiel la unue metita disko, aŭ sur la alia. La unuan eblon ni nomu X, la alian Y.
Por "turo" el unu disko la afero estas facila: Necesas meti ĝin al B, kaj per tio jam "la tuta turo" staras sur B. Turoj el unu disko do apartenas al X.
Ni nun supozu, ke por iu N la turoj de alto N−1 apartenas al X. Ĉar ni ja volas meti la N-turon al B, ni devas en la dua paŝo meti la plej grandan diskon al B; do en la unua paŝo ni devas meti la sub-turon al P. ĉar la sub-turo apartenas al X, ni devas meti ĝian unuan diskon same al P, kaj tio signifas, ke turoj de alto N apartenas al Y (ni komencas per P kaj alvenas sur B).
Analoge eblas pruvi, ke N-turoj apartenas al X, se N−1-turoj apartenas al Y. Ĉar la alto 1 apartenas al X, 2 do apartenas al Y; pro tio 3 apartenas al X ktp. Tio kondukas al jena regulo: