Enkonduko en la aŭtomatan daten-prilaboradon (2)
Enkonduko en la aŭtomatan daten-prilaboradon (2)
Tre konata apliko de komputiloj estas kalkul-tabeloj. Laŭ la angla esprimo spreadsheet ili foje estas nomataj "stern-tabeloj", sed tio estas malpli preciza vorto.
Kalkultabelo estas du-dimensia tabelo, kies ĉeloj (kampoj) kutime enhavas nombrojn. Ofte la horizontaloj (linioj) estas numerataj per nombroj kaj la vertikaloj (kolumnoj) per latinaj literoj. Ĉar ekzistas nur 26 latinaj literoj, oni uzas ankaŭ parojn de literoj (kvazaŭ literoj estus ciferoj):
| A | B | C | … | Y | Z | AA | AB | … | AZ | BA | … | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ||||||||||||
| 2 | ||||||||||||
| … |
La diferenco inter normala tabelo kaj kalkultabelo estas, ke en kalkultabelo la valoroj en la ĉeloj povas dependi de la valoroj en aliaj ĉeloj. Ekzemple en iu ĉelo povas esti la sumo de du aliaj ĉeloj.
Konataj ekzemploj de kalkul-tabelaj (aŭ tabel-kalkulaj) programoj estas:
Tabelkalkuliloj havis grandan signifon por la historia evoluo de komputiloj, ĉar ili unue permesis al ne-programistoj kalkuli per komputilo.
La uzo de tabelkalkulado estas parto de la "Eŭropa Komputila Konduk-Permesilo". Interese estas, ke la ekzameno por tiu permesilo komence postulis la spertecon ne pri iu ajn tabelkalkulilo, sed speciale pri Microsoft Excel. Intertempe ĝi akceptas ankaŭ la programaron StarOffice, kiu estas kongrua al OpenOffice.
Tiu ĉi ĉapitro kaj la sekvantaj baziĝas sur OpenOffice kaj la programo Calc. La diferencoj al aliaj kalkul-programoj tamen ne estas tre grandaj.
Kiam oni kreas novan kalkul-tabelon, aperas bildo simila al jena:
Malsupre estas la plej grava elemento, la tabelo kun la numeritaj vertikaloj kaj horizontaloj. Super ĝi, dekstre de la simbolo "=", estas teksto-linio, kiu montras la enhavon de la elektita ĉelo. Elekti ĉelon oni povas per alklako per la muso, aŭ per navigado per la klavaro. Por tio ĉi oni povas uzi la sago-klavojn kaj la tab-klavaro, kiu saltas dekstren al la sekva vertikalo.
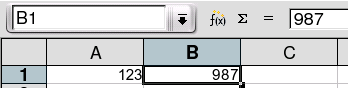
Kiam oni entajpas simplan tekston en ĉelon, ĝi tie aperas. Ekzemple oni povas tajpi en la unuan ĉelon (A1) la nombron "123" kaj en la apudan ĉelon (B1) la nombron "987". La tabelo tiam aspektas jene:
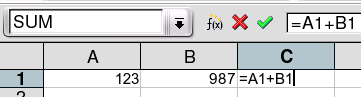
Por vere kalkuli oni devas tajpi la signon "=" en la komenco de ĉelo. Tion oni povas fari per la klavaro aŭ klakante la simbolon "=" super la tabelo. Ni elektu ĉelon C1, uzu la klavaron kaj tajpu "=A1+B1". Super la tabelo aperas verda hoketo:
Kiam ni klakas al la verda hoko, en ĉelo C1 aperas la rezulto de la kalkulado: La sumo 1110 (= 123 + 987):
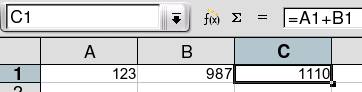
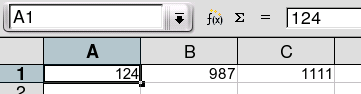
Grava eco estas, ke la programo ne simple faris la kalkulon kaj forgesis, kiel la rezulto ekestis: La linio super la tabelo ankoraŭ montras la formulon "=A1+B1". Nur la ĉelo montras la rezulton "1110". Ke tiu diferenco estas grava, ni vidas, se ni ŝanĝas la valoron en ĉelo A1 al "124" (kaj ne forgesas alklaki la verdan hoketon): En ĉelo C1, kiun ni tute ne modifis, aperas la nova sumo "1111":
Tiu ĉi kapablo, kalkuli ĉelojn el aliaj ĉeloj, estas la centra elemento de tabelkalkuliloj. Kutime ili havas multe da aliaj kapabloj, sed ili servas nur por igi la uzadon pli komforta.
Kompreneble la adicio (+) ne estas la sola operacio de tabelkalkuliloj. Oni povas uzi ne nur ĉiujn kvar bazajn aritmetikajn operaciojn (adico, subtraho, multipliko, divido per la signoj +, −, * kaj /), sed ankaŭ multajn pli komplikajn funkciojn. Listo de tiuj funkcioj aperas, kiam oni klakas al la simbolo "f(x)" super la tabelo. Jen kelkaj ekzemploj:
| Operacioj de tabelkalkulilo | |||
|---|---|---|---|
| nomo | priskribo | ekzemplo | rezulto |
| ABS | absoluta (pozitiva) valoro de nombro aŭ esprimo | ABS(−22) | 22 |
| COUNT | nombro de la donitaj elementoj | COUNT(11, 297, 75) | 3 |
| DAYS | tagoj inter du datoj | DAYS(B2;A2) | tagoj inter la datoj en B2 kaj A2 |
| SUM | sumo de pluraj valoroj | SUM(A1:C1) SUM(11; 22; 33) |
sumo de A1, B1 kaj C1 66 |
La lasta ekzemplo montras, ke la funkcioj povas uzi rektajn valorojn (ekz. "11") kaj ankaŭ la valorojn en aliaj ĉeloj (ekz. "A1"). La signo ";" (punkto-komo, en kelkaj lingvoj estas la komo) disigas valorojn. La signo ":" (dupunkto) indikas vicon da valoroj, kiuj staras en unu vertikalo ("A1:A25"), unu horizontalo ("A1:Y1") aŭ en ort-angula areo ("=SUM(A1:D3)" adicias 12 valorojn en areo de 4×3 ĉeloj).
Tre utila estas la kapablo transpreni formulojn al aliaj horizontaloj aŭ vertikaloj. Ni supozu, ke ni volas kalkuli la perimetrojn kaj la areojn de cirklo el la radiuso. Por tio ni tajpas jenajn valorojn kaj formulojn:
| A2 | B2 | C2 | |
|---|---|---|---|
| teksto | 1 | =A2 * 2 * 3,14159 | =A2 * A2 * 3.14159 |
| signifo | la radiuso | la formulo de la perimetro | la formulo de la areo |
Se ni havas plurajn cirklojn, ni povas entajpi iliajn radiusojn en la unua kolumno sub A2. Tiam ni elektas la formulajn ĉelojn B2 kaj C2 (mus-premo al B2, mus-tiro al C2) kaj per la muso tiras la dekstran malsupran angulon de C2 malsupren (aperas ruĝa kadro:
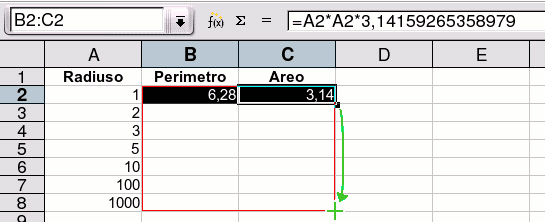
Kiam ni lasas la musbutonon, niaj formuloj estis kopiitaj al la tuta kadro, kaj kun la ĝustaj adaptoj: B3 kaj C3 uzas la radiuson el A3 ktp:
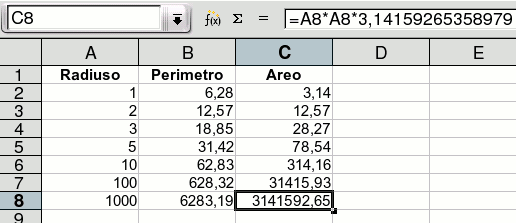
La ĝisnunaj ekzemploj estis simplaj, sed kalkultabeloj povas enhavi tre kompleksajn strukturojn. Speciale, la ĉeloj, kiuj estas uzataj en formuloj, mem povas enhavi formulojn ktp.
Ni konsideru ekzemplan tabelon kun la kostoj de iu varo. En la unua horizontalo troviĝas tri ĝeneralaj valoroj:
Sub tiu horizontalo estas tabelo kun la kostoj por diversaj kvantoj de la varo:
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | prezo de unu peco: | prezo de afranko: | procenta imposto: | |||
| 2 | nombro de pecoj | prezo de ĉiuj pecoj | kosto de varo plus afranko |
valoro de imposto | suma prezo | |
| 3 | =A3*B1 | =B3+D1 | =C3*F1/100 | =C3+D3 | ||
| 4 | =A4*B1 | =B4+D1 | =C4*F1/100 | =C4+D4 | ||
| 5 | =A5*B1 | =B5+D1 | =C5*F1/100 | =C5+D5 | ||
| … | ||||||
Kun la valoroj 9,90 (prezo), 20,00 (afranko) kaj 13 % (imposto) rezultas ekzemple jena tabelo:
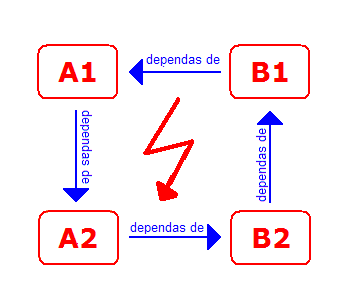
Multaj ĉeloj dependas de aliaj. Precipe de la tri valoroj en la unua horizontalo dependas preskaŭ ĉio; se oni ŝanĝas la prezon de unu peco, la tuta tabelo iĝas alia. Tiuj dependecoj formas tutan reton en la tabelo, kaj tiu reto povas esti kompleksa. Tamen la programo devas konstante aktualigi la tutan tabelon, kiam io ŝanĝiĝas. Kiel tio eblas?
Grava fakto estas, ke ĉiam nur unu ĉelo (la elektita ĉelo; ni nomu ĝin X) povas ŝanĝiĝi samtempe. Tiu ĉelo povas enhavi formulon, kiu dependas de aliaj ĉeloj.
Tio estas rikura procedo: En la tria paŝo oni traktas la rekalkulitajn ĉelojn tiel, kiel en la dua oni traktas X, kaj same en la pluaj paŝoj. Ĉu tiu kalkulado iam finiĝos? Jes; ĉiu ĉelo povas ja nur unufoje ŝanĝiĝi, kaj ekzistas nur finia nombro da ĉeloj.
Ni rigardu denove la ĉelojn de nia ekzemplo. La ĉeloj, kiuj dependas de la afranko (D1), formas hierarkion (arbon), kies radiko estas D1. Kiam la valoro de D1 ŝanĝiĝas, necesas sekvi tiun hierarkion: Unue necesas rekalkuli C3, C4, C5 ktp., kiuj dependas de D1. Tiam necesas rekalkuli D3 kaj E3, kiuj dependas de C3. Tiam necesas rekalkuli D4 kaj E4, kiuj dependas de C4. Kaj tiel plu. Por la ĉelo F1 jena bildo montras la hierarkion:
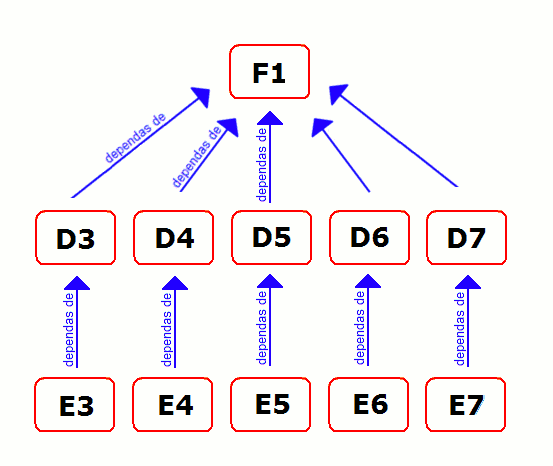
Kiam la uzanto de la programo ŝanĝas unu valoron en unu ĉelo X, la programo do devas plenumi du paŝojn:
Ĉar ĉiam nur unu ĉelo povas ŝanĝi sian valoron, la programo bezonas rigardi ĝiam nur tiun hierarkion. Tio estas multe pli simpla ol rigardi la tutan reton da dependecoj.
Tute precize, la ĉeloj, kiuj dependas de iu ĉelo X, ne ĉiam formas veran hierarkion. Ekzemple povas esti, ke du branĉoj de la "arbo" kunkreskas. Ni rigardu la ekzemplon de kalkulfolio, kiu kalkulas polinomon:
La koeficientojn 7, 5 kaj 8 ni skribu en la unuan horizontalon; sub ili estu la potencoj de x, sub ili la produtoj de la koeficientoj kaj la potencoj. Dekstre, en ĉelo D3, estu la rezulto y.
| A | B | C | ||
|---|---|---|---|---|
| 1 | 7 | 5 | 8 | |
| 2 | 1 | x | =B2*B2 | |
| 3 | =A1*A2 | =B1*B2 | =C1*C2 | =A3+B3+C3 |
| A | B | C | ||
|---|---|---|---|---|
| 1 | 7 | 5 | 8 | |
| 2 | 1 | x | x2 | |
| 3 | 7 | 5x | 8x2 | 7 + 5x + 8x2 |
La ĉelo C2, kun la variablo x, influas multajn aliajn ĉelojn, sed ne en la formo de pura hierarkio. La dependo-grafo apartenas al pli ĝenerala klaso da grafoj, kiuj nomiĝas direktitaj ne-ciklaj grafoj. Mallonge oni nomas ilin "dingoj" (DIrektitaj Ne-ciklaj GrafOJ), en kelkaj lingvoj ili nomiĝas dag, laŭ mallongigo de la angla esprimo directed acyclic graph. "Ciklo" estas vojo en grafo, kiu revenas al sia komenco. En arbo ne ekzistas cikloj; en dingo ili povas ekzisti, sed nur, se la vojo parte iras "kontraŭ la direkto" de la eĝoj. La direkton oni difinas per la radiko; estas egale, ĉu oni distingas la direkton al la radiko aŭ de la radiko.
La dependo-grafo de la polinoma ekzemplo havas ciklojn; ankaŭ tiu de la prez-tabela ekzemplo, el kiu ni konsideru nur la 3-an horizontalon (kaj la unuan):
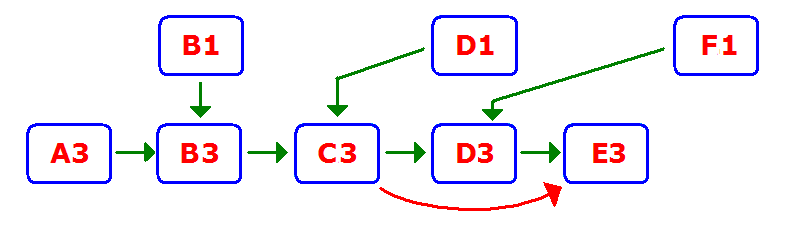
Kiel ni vidas laŭ la ekzemplo, en dingo povas esti pli ol unu vojo de vertico al la radiko (tio ne povas okazi en arbo): En la dependo-grafo de C3 la radiko (C3) estas ligita al E3 tra D3, sed ankaŭ rekte. Se la eĝoj ne havus direkton (al la radiko), la grafoj en la ekzemploj havus ciklon.
Ĉu la dependo-strukturo de ĉelo en kalkul-tabelo povas enhavi veran ciklon? Oni povas konstrui tiajn tabelojn, sed ili ne havas sencon, ĉar ili ne estas kalkuleblaj. Oni ja bezonas almenaŭ unu ĉelon kun konstanta valoro, ĉe kiu povas finiĝi la kalkulado. Tial la jena tabelo estas sensenca; kalkulprogramoj rifuzas kalkuli ĝin:
| ne funkcias! | A | B |
|---|---|---|
| 1 | =A2+1 | =A1+1 |
| 2 | =B2+1 | =B1+1 |