Zur Lösung dieses Problems dienen Zertifikate. Sie werden von einer vertrauenswürdigen Stelle (was immer das heißt) ausgestellt und bescheinigen mit deren Signatur, dass
Es lassen sich ganze Hierarchien von Zertifikaten aufbauen, indem ZSen die Signaturen untergeordneter (zum Beispiel lokaler) ZAs beglaubigen. Große ZSen werden ihre Schlüssel gegenseitig beglaubigen. Es genügt dann, wenn jeder Teilnehmer am System den öffentlichen Schlüssel einer einzigen ZS verlässlich kennt. Zur Sicherheit sollte sie in einem nicht manipulierbaren Speicher gehalten werden, etwa in einer Chip-Karte, die durch ein PIN (persönliche Identifizierungnummer) gesichert ist. Diese Chip-Karte hält natürlich auch den privaten Schlüssel des Eigentümers, mit dem er Nachrichten signiert und empfangene Nachrichten entschlüsselt.
Eine Signatur kann alles beglaubigen, was im Papierverkehr unterschrieben wird: einen Vertrag, einen Scheck, eine Überweisung, einen Brief. Lediglich einem Zweck kann sie, im Gegensatz zur traditionellen Unterschrift, nicht dienen: Der Bestätigung einer Änderung an einem bereits signierten Dokument. Der Grund dafür ist, dass dieses signierte Dokument bereits kopiert worden sein könnte, und auf die Kopien hat die Änderung natürlich keinen Einfluss. Ein Beispiel: Wäre der Personalausweis ein digitales, von der Behörde digital signiertes Dokument, so könnte man darauf bei einem Umzug keinen neuen Wohnsitz eintragen; der Besitzer hätte dann zwei Personalausweise, einen mit dem alten und einen mit dem neuen Wohnsitz. Aus demselben Grund könnte man jemandem nicht, um ihm wirksam die Fahrerlaubnis zu entziehen, den digitalen Führerschein wegnehmen.
Die perfekte Kopierbarkeit digitaler Nachrichten muss auch an anderen Stellen berücksichtigt werden. Wenn ein digitaler Scheck eingelöst wird, muss geprüft werden, ob eine Kopie davon nicht bereits eingelöst wurde. Das ist nur durch Rückfrage bei einer gut erreichbaren Zentrale möglich. Digitale Barschecks sind daher nicht sehr praktisch; bei Verrechnungsschecks hat man mehr Zeit zum Prüfen, aber auch dabei besteht das Problem herauszufinden, wer der rechtmäße Vorleger ist. Idealerweise verwendet man daher keine digitalen Schecks, sondern digitale Überweisungen mit eingetragenem Empfänger, fortlaufender Nummer sowie Datum und Uhrzeit. Auch solche Überweisungen können dem Empfänger als Zahlungsmittel übergeben oder übersandt werden, der sie dann seiner Bank zur Gutschrift vorlegen kann.
Das Problem digitalen Bargelds wird weiter unten behandelt.
Das ist im Prinzip möglich, indem man eine Nachricht, die der Partner schickt, mit seinem privaten Schlüssel chiffriert, was der Partner dann mit dem öffentlichen Schlüssel überprüfen kann. Weil diese Nachricht sozusagen eine Herausforderung darstellt, die man entsprechend beantworten muss, heißt ein solches Verfahren englisch challenge and response.
Ganz unproblematisch ist dieses Szenario nicht, denn wenn man blindlings signiert, was der Partner schickt, könnte dieser Nachrichten schicken, aus deren Signatur er Vorteil ziehen könnte; beispielsweise könnte er einen Scheck signieren lassen. Man wird daher gewöhnlich etwas Unverfängliches signieren, etwa Datum und Uhrzeit. Zumindest sollten solche Nachrichten einen vom Signierer bestimmten Vorspann enthalten und in der Länge begrenzt sein.
Ein besseres Verfahren ist weiter unten beschrieben.
In so einem Fall muss der private Schlüssel in der Chipkarte widerrufen werden, da Nachrichten, die ab diesem Zeitpunkt damit signiert wurden, nicht mehr sicher dem Eigentümer des Schlüssels zugeschrieben werden können.
Leider sieht man einer Nachricht nicht so einfach an, wann sie signiert wurde, insbesondere also vor oder nach der Kompromittierung des Schlüssels. Daher werden mit dem Widerruf des Schlüssels eigentlich alle, auch früher, mit dem Schlüssel erzeugten Signaturen wertlos. Sie könnten ja, gegebenenfalls mit falscher Zeitangabe, später mit der geraubten Signatur erzeugt worden sein.
Dieser Sachverhalt ist sehr unangenehm, denn er bedroht alle bestehenden Signaturen mit der jederzeitigen Möglichkeit, wertlos zu werden. Daher sollten wichtige Signaturen, zum Beispiel an Verträgen mit längerfristiger Bedeutung, gesichert werden, und zwar durch eine Art notarielle Beglaubigung. Diese geschieht dadurch, dass eine vertrauenswürdige Stelle, gewöhnlich eine ZS, mit ihrem Schlüssel die signierte Nachricht zusammen mit Datum und Uhrzeit signiert. Damit lässt sich im Bedarfsfall beweisen, dass eine Signatur vor dem Widerruf des Schlüssels erzeugt wurde, also gültig ist.
Außerordentlich unangenehm wäre es natürlich, wenn der Schlüssel einer ZS widerrufen werden müsste. Solche Schlüssel sollten natürlich besonders gut gesichert werden und möglichst ein gesichertes Firmengelände oder Rechenzentrum nicht verlassen. Zur besonderen Sicherheit kann man eine Nachricht von mehreren ZSen beglaubigen lassen. Zur Schadensbegrenzung könnte man die Schlüssel einer ZS noch regelmäßig wechseln und dabei den privaten Schlüssel vernichten; das würde jedoch jedesmal die Verteilung eines neuen öffentlichen Schlüssels erfordern und wäre daher unpraktisch.
Wie lässt sich solches anonymes Bargeld überhaupt herstellen? Es muss ja irgendwo gegen andere Werte einlösbar sein, und das kann nicht beim Ausgeber sein, der ja anonym bleiben will. Es muss eine Art Notenbank geben, die digitales Bargeld ausgibt und bei Bedarf auch wieder einlöst. Dieses Bargeld gibt sie natürlich nur gegen eine Abbuchung auf einem Konto her. Wie kann der Abheber aber sicher sein, dass die Bank nicht die Nummer der digitalen Banknote (die ja letztlich nichts weiter als eine Nummer ist) notiert, so dass sie später nach dem Ausgeben zu ihm zurückzuverfolgen ist?
Um das zu verstehen, denken wir uns ein etwas seltsames Land, in dem die Notenbank die Geldscheine auf Papier druckt, das der Bankkunde mitbringt. Wenn die Bank dieses Papier sehen könnte, könnte sie sine Fasermuster usw. registrieren und die Banknote wiedererkennen. Legt der Kunde aber das Papier zusammen mit einem Kohlepapier in einen Umschlag, so kann die Notenbank durch den Umschlag und das Kohlepapier hindurchdrucken, ohne das Papier jemals zu sehen.
Dieses ziemlich unrealistische Szenario gewinnt sofort an Realisierbarkeit, wenn man es ins Digitale überträgt. Die Notenbank (oder eine andere Bank) stellt Bargeld dadurch aus, dass sie riesig große Phantasiezahlen mit einer speziellen Geld-Signatur signiert. Wird die so signierte Zahl der Bank wieder vorgelegt, so zahlt sie den Betrag aus. (Zum Problem des doppelten Vorlegens weiter unten.)
Anstatt nun eine Zahl offen vorzulegen, so dass die Bank sie zusammen mit dem Namen des Abhebers registrieren könnte, verschlüsselt dieser die Zahl zusammen mit seinem öffentlichen Schlüssel. Da zum Entschlüsseln der private Schlüssel nötig ist, kann die Bank die ursprüngliche Zahl nicht kennen; sie signiert nun die verschlüsselte Zahl mit dem Geld-Schlüssel. Nun kommt der Clou: Bei bestimmten Verschlüsselungen spielt die Reihenfolge der Chiffrierungen keine Rolle! Der Abheber entschlüsselt nun die Banknote mit seinem privaten Schlüssel, wobei die Geld-Signatur nicht verlorengeht! Er hat nun eine geld-signierte Zahl, die niemand kennt als er, und kann sie ausgeben, ohne dass die Note zu ihm zurückverfolgt werden kann. (Man müsste versuchsweise alle ausgegebenen Noten mit seinem öffentlichen Schlüssel verschlüsseln, um gerade seine zu finden.)
In dieser Form ist das Verfahren natürlich undurchführbar, denn wenn der Abheber die Note mehrfach ausgibt, könnte man ihn ja nicht ertappen, außer man überprüft jede Note sofort beim Geldtransfer. Es gibt aber Tricks, Abhebe- und Bezahlvorgang so zu gestalten, dass ein doppeltes Ausgeben der Note doch eine Feststellung des Ausgebers erlauben würde.
Solche Konzepte für digitales Bargeld sind kaum gegen den Fall zu schützen, dass ein Betrüger sich in ein Land zurückzieht, das Wirtschaftsverbrecher nicht ausliefert. Zieht man andererseits in Betracht, dass Kreditkartenbetrüger bereits heutzutage kaum ein Risiko eingehen und trotzdem das Geschäft mit Kreditkarten floriert, so muss das kein Hindernis für die Einführung digitalen Bargelds darstellen.
Solche Fasern müssen optisch, magnetisch oder wie auch immer erfasst und in digitale Form gebracht werden; dabei muss eine gewisse Toleranz walten, damit Abnutzungen am Papier die Werte nicht verfälschen. Das digitale Resultat wird mit dem privaten Schlüssel der Notenbank verschlüsselt und das Ergebnis auf die Note aufgedruckt. Zur Prüfung der Echtheit dechiffriert man die aufgedruckte Nummer und vergleicht sie mit dem erneut gemessenen Fasermuster.
Wurde die Note einfach gefälscht, also mit einer Fantasiesignatur versehen, so ist scheitert diese natürlich an der Prüfung (außer bei astronomisch viel Glück). Wurde die Note aber samt Signatur kopiert, so hat das Papier der Kopie ein anderes Fasermuster, so dass die Signatur ebenfalls nicht stimmt. Da sich das Fasermuster nur in Grenzen willkürlich beeinflussen lässt, kann der Fälscher das Originalpapier nicht bis ins Fasermuster hinein kopieren.
Eine bessere Möglichkeit stellen sog. Null-Wissen-Beweise (zero knowledge proof) dar. Dabei kann sich ein Herausforderer A zwar überzeugen, dass der Herausgeforderte B tatsächlich im Besitz eines Geheimnisses ist, gewinnt dabei jedoch keinerlei Einblick in das Geheimnis und kann auch gegenüber Dritten nicht beweisen, dass B sich ihm ausgewiesen hat. B hat in diesem Sinne eine Art Anonymität gewahrt.
Ohne auf mathematische Verfahren einzugehen,
kann man die Null-Wissen-Beweise durch ein seltsames Haus
veranschaulichen, das aus zwei Zimmern (ohne Fenster) besteht.
Jedes hat eine Eingangstür Ei zur Vorder-
und eine Ausgangstür Ai zur Hinterseite.
Die Eingangstüren lassen sich von außen verriegeln.
Außerdem gibt es eine Verbindungstür V,
die ein Geheimschloss besitzt.
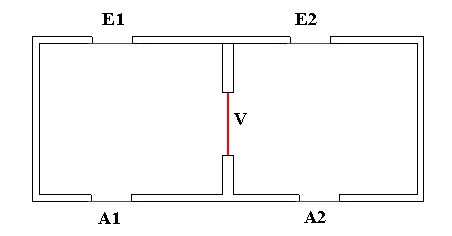
B beweist A, dass er das Geheimschloss öffnen kann, ohne ihn dabei zusehen zu lassen: A bleibt vor dem Haus stehen, während B ungesehen durch eine der hinteren Türen hineingeht. Anschließend verriegelt A die Eingangstüren, wählt eine der beiden Vordertüren und ruft B die Wahl hinein; B hat nun die Aufgabe, durch diese Tür herauszukommen. Wenn er das Geheimschloss öffnen kann, ist das kein Problem für ihn; sonst kann er es nur mit 50 % Wahrscheinlichkeit. Nach mehreren erfolgreichen Versuchen wird A überzeugt sein, dass B das Geheimnis kennt. Aber selbst wenn A den ganzen Vorgang auf Video aufnimmt, kann er niemandem Beweisen, dass B das Geheimnis wirklich kennt; denn die Szene würde genauso aussehen, wenn er sich mit B vorher abgesprochen hätte, wann er welche Tür wählt.