Authentisierung durch Wissen

Sehr stark vereinfachend kann man sagen:

Wissen = Daten

Authentisierung durch Wissen ist daher für Datenverarbeitung gut geeignet.

Das gilt sogar für den Fall "prozeduralen" Wissens.

Beispiel: Bankgeschäfte per PC

(auf Deutsch: home banking, electronic banking)

Im Gegensatz zur traditionellen Papierform fehlen das Formular und die Unterschrift.

Problem: Ist es wirklich der Kontoinhaber, der eine Überweisung tätigt?
Lösung: PIN (persönliche Identifikations-Nummer)
Problem: PIN kann abgehört werden.
Lösung: TAN (Transaktionsnummer), wird nur einmal verwendet.
Problem: Die Bank weist sich nicht aus. Es könnte sein, dass am anderen Ende nicht der Bank-Computer "spricht", sondern der Bösewicht, der nur die TAN erfahren möchte.
Lösung: Telefonnetz "garantiert" richtige Verbindung.
Problem: Überweisung kann auf dem Weg vom Kunden-PC zur Bank verfälscht werden (Betrag, Kontonummer).
Lösung: Telefonnetz "garantiert" richtige Übertragung.
Problem: Bank könnte Überweisung verfälschen. Da sie alle TANs kennt, kann sie sogar falsche Überweisungen ausstellen.
Lösung: Das wird sie doch nicht tun!

Festzuhalten: Wer per PC überweist, gibt sich vollständig in die Hände seiner Bank.

Das Geheimnis des Tartaglia

zeigt, dass man den Besitz eines Geheimnisses prüfen kann, ohne es selbst zu kennen:

Tartaglia entdeckte die Cardanosche Formel zur Lösung von Gleichungen dritten Grades:

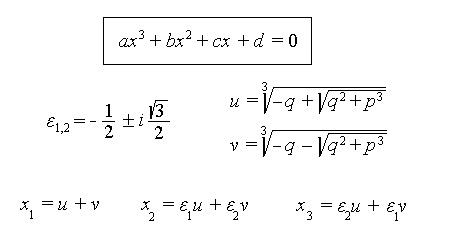
Er verriet sie aber niemandem. Trotzdem konnte er überzeugend behaupten, eine solche Formel zu kennen, da er alle ihm vorgelegten Gleichungen dritten Grades lösen konnte.

Entscheidend: Es ist leicht zu prüfen, ob eine gegebene Zahl eine Gleichung dritten Grades löst.

Leider kann nicht jeder eine solche geheime Formel erfinden. "Öffentlich überprüfbare" Geheimnisse lassen sich aber produzieren, wenn man "Einweg-Funktionen" kennt:

Eine Funktion heißt Einweg-Funktion, wenn sie mit geringem Aufwand berechenbar, aber nicht mit vertretbarem Aufwand umkehrbar ist.

Funktionen, von denen man vermutet, dass es Einweg-Funktionen sind:

die Multiplikation von ganzen Zahlen (Umkehrung: Primfaktorzerlegung)
die ganzzahlige Potenzierung modulo N (Umkehrung: der ganzzahlige Logarithmus)