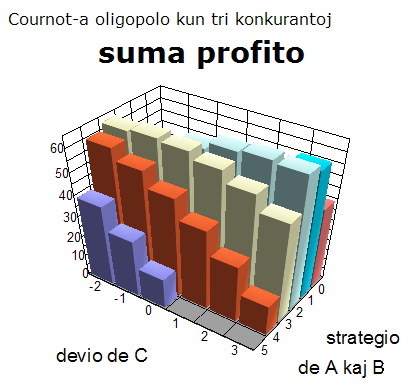
Suma profito en la oligopolo
Same kiel statistiko, ludoteorio havas rilaton al filozofio. Ĝi ne povas decidi pri siaj celoj, ekzemple diri ĉu ludo "estu" justa, ĉu homoj estas "raciaj agantoj", kiuj atentas nur siajn proprajn interesojn, ktp. Ĝi certe ne povas diri, kiuj estas la interesoj de iu ludanto. Tiaj konsideroj estas filozofiaj demandoj, decidendaj ekster la ludoteorio.
La ludoteorio nur povas (eventuale) diri, ĉu iu filozofia celo estas atingebla, kaj kiel. Tiel ĝi iusence respondas ankaŭ filozofiajn demandojn.
Ludoteoria artikolo de Xavier Hubaut analizas situacion el la Dua Mondmilito, en kiu la Germana generalo Günther von Kluge devis decidi, ĉu retiriĝi malantaŭ la Sejnon aŭ ataki la aliancan generalon Omar Bradley, kiu siaflanke devis decidi inter tri ebloj:
Hubaut donas jenan matricon por la rezultoj de la ludo el la alianca vidpunkto:
| GvK atakas | GvK retiriĝas | |
|---|---|---|
| OB vokas rezervojn | 2 | 3 |
| OB progresas | 1 | 5 |
| OB atendas | 6 | 4 |
Ĉi-tie ni ne volas analizi la ludon, sed simple montri la limojn de la ludo-teorio: Ĝi povas nek provizi la eblajn strategiojn nek doni la rezultojn, do ĝi neniel povas helpi en la kompilado de la ĉi-supra matrico. Nur poste ĝi povas doni helpon por decidi.
Ni revenu al la citita ekzemplo de la Cournot-a oligopolo: tri produktantoj konkurencas pri merkato, kiu pagas por varo (18 - n) mon-unuojn, se la propono estas n (pecoj, ekzempleroj). La ludoteorio ne povas diri, ĉu tia situacio estas iel realisma. La ludo estas interesa, ĉar la homa intuicio ŝajne ne facile kapablas decidi pri strategio "bona" – bona por la individua ludanto. Tial estas kutima ludo en ekonomikaj kursoj, ke la partoprenantoj intuicie elektu sian preferatan strategion antaŭ la analizo de la ludo.
La ludoterio ne kapablas diri, ĉu la boneco de strategio, t. e la maksimumigo de la profito, estas bona laŭ aliaj vidpunktoj, ekz. el tiu de la popol-ekonomio, aŭ tiu de ekonomia daŭremo.
La tri "ludantoj" decidas individue, kiom de la varo ili produktas (kaj proponas al la merkato). Evidente ne utilas produkti 18 aŭ pli (tio nuligus la prezon); eĉ la strategio 17 estas eliminebla, ĉar la produktado-kostoj de 2 negativigus la profiton. ĉiu ludanto havas maksimume 17 strategiojn, nome produkti 0, 1, .., 16. Prezenti la tridimensian strategi-spacon kun la 16³ = 4096 rezultoj estas malfacile; ni do koncentriĝu je parto, en kiu du ludantoj uzas la saman strategion kaj la tria provas devii de ĝi. Por ĉiu strategi-kombino ni prezentas la rezultantan prezon, la suman profiton kaj la tri individuajn profitojn:
|
prezo; suma profito; (profito de A/profito de B/profito de C) |
| ludanto C devias je... | |||||||
|---|---|---|---|---|---|---|---|
| -2 | -1 | 0 | 1 | 2 | 3 | ||
| ludantoj A kaj B ludas... |
0 | – | – | 18; 0 (0/0/0) |
17; 15 (0/0/15) |
16; 28 (0/0/28) |
15; 39 (0/0/39) |
| 1 | – | 16; 28 (14/14/0) |
15; 39 (13/13/13) |
14; 48 (12/12/24) |
13; 55 (11/11/33) |
12; 60 (10/10/40) |
|
| 2 | 14; 48 (24/24/0) |
13; 55 (22/22/11) |
12; 60 (20/20/20) |
11; 63 (18/18/27) |
10;
64 (16/16/32) |
9; 63 (14/14/35) |
|
| 3 | 11; 63 (27/27/9) |
10;
64 (24/24/16) |
9; 63 (21/21/21) |
8; 60 (18/18/24) |
7; 55 (15/15/25) |
6; 48 (12/12/24) |
|
| 4 | 8; 60 (24/24/12) |
7; 55 (20/20/15) |
6; 48 (16/16/16) |
5; 39 (12/12/15) |
4; 28 (8/8/12) |
3; 15 (4/4/7) |
|
| 5 | 5; 39 (15/15/9) |
4; 28 (10/10/8) |
3; 15 (5/5/5) |
2; 0 (0/0/0) |
1; -17 (-5/-5/-7) |
× | |
| 6 | 2; 0 (0/0/0) |
1; -17 (-6/-6/-5) |
× | × | × | × | |
La strekoj signifas, ke tia ludo ne eblas (ne eblas negativa produktado); la ×-oj estas mallongigo por rezulto kun nula prezo kaj do negativa profito. La prezentado ne de la strategio de C, sed de ties devio, sugestas, ke pro la simetrieco de la ludo la tri konkurantoj agu pli-malpli egale, por ke la ludo estu "justa". Tamen justeco ne estas en la intereso de la unuopaj ludantoj, kiuj individue preferus maksimuman maljustecon, nome mem ricevi ĉiom.
Kiel procedi por analizi tiun ludon? Unue konstateblas, ke la suma pago (profito) ne estas konstanta; ĝi estas nula por proponado n de 0 kaj 17 kaj pozitiva inter tiuj du valoroj, nome n(18-n)-2n = 16n-n². La maksimumo de tiu pago-funkcio estas ĉe n=8 kaj havas valoron de 64.
Tiu maksimuma suma pago efektive aperas ĉe la strategiaro (2/2/4), kiu donas pagojn de (16/16/32), kaj ĉe (3/3/2) kun pagoj de (24/24/16). Preskaŭ la maksimumon donas la simetria punkto (3/3/3), kiu pagas (21/21/21), do sume 63. Sed ĉiu ludanto povas plibonigi sian individuan pagon, je la kosto de la konkurantoj, al 24 (3/3/4) aŭ eĉ 25 (3/3/5).
La strategi-kombino (3/3/3) estas do nestabila. Ludantoj emas kreskigi sian produktadon tiom, kiom tio ankoraŭ altigas la profiton. Tio ne eblas por la strategiaro (4/4/4), kie ajna devio kaŭzas malpli grandan pagon por la devianto. Tiu punkto do estas stabila: Neniu ludanto havas intereson devii de ĝi.
La ludo posedas kelkajn instruajn ecojn:
La sekvaj grafoj montras, kiel la suma profito kaj la profito de C kreskas kaj malkreskas laŭ la devio de C de "komuna" strategio, sed ne egale por malsamaj strategioj de A kaj B. Tio kaŭzas konflikton inter la komuna intereso kaj la intereso de la devianto kaj kondukas al diferenco inter la stabilaj punktoj kaj la punktoj de maksimuma suma profito.

Suma profito en la oligopolo
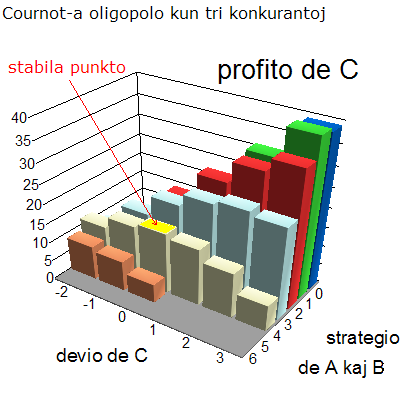
Profito de la devianta ludanto en la oligopolo
Oni povas demandi, kial la punkto (4/4/4) estas stabila kaj la punkto (3/3/3) ne. Por kompreni tion ni rigardu la konsekvencojn de altigo de la produktado je 1 peco: En la punkto (3/3/3) tio malaltigas la pecan prezon de 7 al 6, do tiu, kiu altigas sian produktadon, altigas sian profiton de (3×5) = 15 al (4×4) = 16. Kontraŭe en (4/4/4) tia altigo malaltigas la pecan prezon de 4 al 3, kaj tiu, kiu produktas unu pecon pli, ŝanĝas sian profiton de (4×2) = 8 al (5×1) = 5, kontraŭ siaj interesoj. Por ke altigo de la suma produktado de 9 al 10 ne havu pozitivan efikon al la individua profito, necesus strategio de minimume 4 (tiam la ŝanĝ restas sen efiko al la profito, ĉar 4×5 = 5×4 = 20); sed se unu ludanto produktas 4 kaj la sumo estas nur 9, tiam nepre la aliaj ludantoj ludas je malpli ol 4 kaj do gajnus per altigo de sia produktado. Tial ĉiu punkto kun suma produktado de 9 estas nestabila.
Kontraŭe en la punkto (4/4/4) neniu havas intereson devii.
|
|
komenco
|
sekva leciono
|