La solvo de Nash
Por la kazo de dupersona ludo Nash proponis,
ke justa solvo por luda kunlaboro devas plenumi
sistemon de kvin aksiomoj,
el kiuj la unuaj du jam estis akceptitaj en la ekonomiko:
- La solvo devas doni al ĉiu ludanto
almenaŭ tiom,
kiom li povus gajni sen kunlaboro
(individua racio).
En nia simpligita formo tio signifas,
ke la solvo devas doni al ĉiu almenaŭ pagon de 0.
Alie iu ludanto, kiu ricevus malpli,
forlasus la interkonsenton.
- La solvo ne estas plibonigebla en la senco,
ke per alia solvo ĉiuj ludantoj ricevu almenaŭ
same kaj unu ricevu eĉ pli
(pareto-optimumeco, kolektiva racio).
-
Se luda situacio estas simetria inter la ludantoj,
ili havu egalan pagon.
-
Se ludo B havas nur parton de la eblaj strategioj de ludo A
kaj la solvo de A estas inter la strategioj de B,
ĝi estas ankaŭ solvo de B
(sendependeco de negravaj ebloj).
-
Se ludo B ekestas el A per multipliko de la pagoj
per fiksaj koeficientoj,
tio validas ankaŭ por la solvoj
(lineareco).
Ni rekonas niajn du kondiĉojn el la antaŭa leciono,
la simetriecon kaj la pareto-optimumecon.
La graveco de ĉi-lasta estas evidenta,
sed montriĝos,
ke la simetrieco gravas eĉ por nesimetriaj ludoj.
La kerna ideo de la solvo de Nash estas transformi
ludon al ekvivalenta simetria (kaj tamen konveksa,
ĉar miksitaj strategioj signifas konveksecon)
ludo,
kiu tiam estas solvebla per la simetrieca aksiomo,
ĝuste kiel ni faris pri la interseksa batalo en
la antaŭa leciono.
Sed se ni simple formus al donita ludo la simetrian tegaĵon
kaj poste ties konveksan tegaĵon,
ni eble aldonus al la ludo punkton,
kiu poste montriĝus la solvo de la simetria ludo,
sed ne estas parto de la origina ludo kaj do ne povas
esti ties solvo,
kiel montras la sekva bildo:
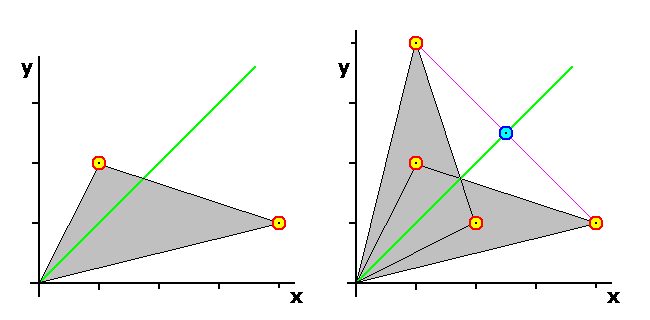
Tian solvon ne eblas retransformi al la origina ludo.
Tial necesas unue (laŭ la aksiomo pri lineareco)
multipliki la pagojn (aŭ almenaŭ tiujn de unu
ludanto)
per faktoro,
kiu certigas,
ke la solvo de la simetria tegaĵo estas ankaŭ
en la nesimetria ludo.
Tiam pro aksiomo 4 ĝi estas ankaŭ ties solvo.
La sekva bildo montras la fazojn de tia transformo-ĉeno:
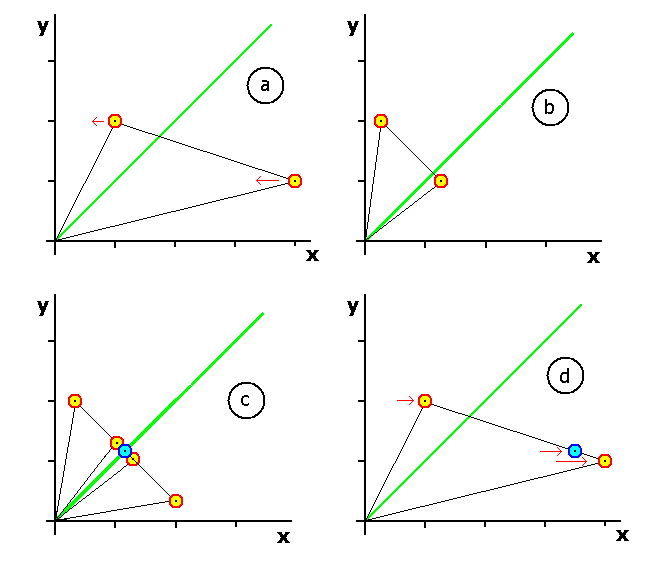
- Bildo a) montras la pago-spacon de la origina ludo;
la pagoj de x estas multiplikitaj per faktoro,
kiu igas la supran-dekstran eĝon orta al
la duoniganto de la kvadranto.
- Bildo b) montras la rezulton.
La supra-dekstra eĝo de la triangulo estas nun
orta al la duoniganto.
- Bildo c) montras la simetriigon per formado de
la simetria tegaĝo.
Ankaŭ ĝi estas konveksa.
Per la simetrieca aksiomo ni povas trovi ĝian solvon,
kiu estas parto de la origina (sed multiplikita) ludo.
- Nun ni povas maligi la multiplikadon,
kaj tiel la solvo de la transformita ludo
transformiĝas al solvo de la origina ludo
(bildo d).
Ni konstatas, ke ĝi tute ne situas en la mezo
inter la du puraj strategioj,
sed multe pli proksime al la maksimuma pago de x.
Sed kiel ni, en la ĝenerala kazo,
sciu, per kio multipliki la pagojn?
Por tio Nash trovis solvon,
kiu kunigas la priskribitajn paŝojn kaj tiel
eĉ evitas la multiplikadon,
kiu ja estas nur dumtempa.
Laŭ Nash ekzistas precize unu solvo,
kiu plenumas la kvin donitajn aksiomojn,
kaj oni trovas ĝin per maksimumigo de la
produto de la du pagoj.
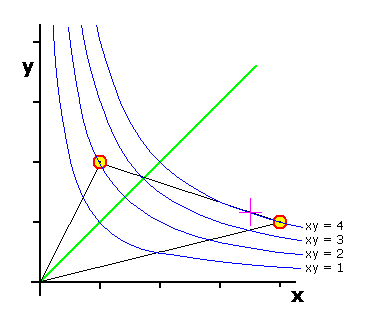
Grafike eblas komprenigi tiun maksimumigon per konstruo de
la hiperbolaro y = a/a por ĉiuj pozitivaj a
kaj trovo de la plej granda a,
kies parabolo ne sekcas (sed tanĝas) la aron de la pagoj.
Por la ĉi-supra ekzemplo rezultas,
ke la maksimuma koordinat-produto,
kiun atingas la rekto tra la du puraj strategioj
(7 - x - 3y = 0),
estas atingita en la punkto x = 3,5
per la valoro
xy = 7/2 × 7/6 = 49/12 = 4,08333...
Denove filozofio
La solvo de Nash estas impresa,
unuavide eble eĉ fascina:
Ŝajnas, ke per ĝi du konkurantoj en ne-konstant-suma ludo
povas interkonsenti pri solvo profitiga por ambaŭ
Necesas tamen konscii,
ke la solvo de Nash ne solvas du aspektojn de tiu problemo:
- Se la solvo ne estas ekvilibro de Nash,
nenio malhelpas, ke unu aŭ ambaŭ ludantoj
deviu de la interkonsentita solvo por profiti;
tio je eblas, alie la solvo estus ekvilibro.
La problemo, kiel devigi plenumon de interkonsento,
estas solvenda ekster la ludo (en alia ludo).
-
La solvo de Nash premisas, ke la du ludantoj interkonsentas
pri la strukturo de la ludo, do ankaŭ pri la pagofunkcio.
Sed en ludoj kia la "batalo de la seksoj" la
ludantoj mem difinas siajn subjektivajn pagojn,
kaj ni vidis,
ke en la "batalo de la seksoj" ja gravas la rilato inter
la pagoj;
se la ludantoj
taksas sian pagon el la du komune vizitataj aranĝoj
je (4;1) kaj (1;2) (kiel en la ĵusa ekzemplo),
la solvo de Nash donas al la unua ludanto
grandan avantaĝon:
la solvo situas tre proksime ĉe la pura strategio
preferata de tiu ludanto,
do tiu strategio rivecas probablon de 5/6 kompare al
1/6 por la pura strategio preferata de la alia ludanto.
La ludantoj do havas motivon aserti tre fortan preferon,
kaj ekestas dua ludo "kiu asertas la plej fortan preferon".
Tio estas evitebla nur en absolute simetriaj ludoj,
sed por tiuj oni ne bezonas la solvon de Nash.
Specimenaj demandoj
-
Kiujn aksiomojn Nash proponis por kalkuli justan interkonsenton
en dupersonaj ludoj?
-
Kion signifas la aksiomo de simetrieco?
-
Kion signifas la aksiomo de sendependeco de negravaj ebloj?
-
Kion signifas la aksiomo de sendependeco de lineareco?
-
Skizu la konstruadon de Nash.
Se vi volas, aldone pruvu,
ke la solvo de Nash (maksimumigi la produton de la pagoj)
vere plenumas la kvin aksiomojn.


