Ni jam plurfoje vidis, ke en ne-konstant-sumaj ludoj la ludantoj ja povus profiti per kunlaboro. Tia kunlaboro postulas unue, ke la ludantoj povu iel komuniki. Krome ili, kiel raciaj agantoj, kunlaboras nur, se tio (iel) estas en ilia (individua) intereso.
La precipa diferenco inter ekvilibroj kaj pareto-optimumoj estas, ke ekvilibroj gravas en strikte konkurencaj situacioj, pareto-optimumoj en situacioj, kie eblas kunlaboro. La diferencon bone montris la ekzemplo de la Cournot-oligopolo. Sed kie aŭ kiel entute eblas "kunlaboro"?
Imagu, ke en la prizonula dilemo la du prizonuloj havas okazon konfidence interparoli dum iom da tempo. Ili promesas al si reciproke ne konfesi. Ĉu tio iel ŝanĝas la situacion? Se prizonulo A kredas, ke prizonulo B estas nefidinda, li ne kredos la promeson kaj do estas en la situacio, elekti inter 20 jaroj kaj 5 jaroj; do li ne plenumos la propran promeson. Sed se li kredas, ke B estas fidinda, li denove estas en la situacio elekti inter 1 jaroj kaj libereco; do kian motivon li havas plenumi sian promeson? Li neniel povas influi la decidon de A.
Por efektivigi kunlaboron (koalicion, aliancon, kartelon) inter du aŭ pluraj ludantoj necesas iu metodo eldevigi la plenumon de farita promeso. Tio povas esti iu supera, potenca instanco, ekzemple ŝtato, kiu punas la neplenumon de kontraktoj – se ili estas laŭleĝaj. En ŝtato subtenanta la liberan merkaton (kio ajn tio estas) do ne eblas fari laŭleĝan kontrakton pri kartelo; tia kontrakto estas per si mem kontraŭleĝa, kaj neniu povas leĝe eldevigi ĝian plenumon. Same en pure anarkia socio ne eblas alvoki superan instancon por eldevigi la plenumon de promeso aŭ kontrakto.
En tia situacio gravas la diferenco inter ludo unufoja kaj ripetebla. Imagu du homojn, kiuj volas efektivigi kontraŭleĝan komercadon tiel, ke unu metas varon en kaŝitan lokon, de kie poste la dua prenas ĝin, lasante interkonsentitan prezon. (Variaĵo diras, ke varon kaj prezon oni lasu samtempe en du malsamaj lokoj, kie poste prenu ilin la respektive alia.) Ni supozu, ke sukcesa komercado donas al ambaŭ profiton, ĉar la varo por la vendanto valoras 9, por la aĉetanto 11, sed estas vendata je 10. La du havas po du strategiojn: La unua (A) povas
La dua aganto (B) povas
La pagomatrico por tiu ludo estas:
| Kaŝa komercado | |||
|---|---|---|---|
| B | |||
| lasas monon | ne lasas monon | ||
| A | lasas varon | 1;1 | -9;11 |
| ne lasas varon | 10;-10 | 0;0 | |
(Evidente estus stulte lasi prezon, ne trovinte varon; sed por kompleteco ni notu ankaŭ tiun eblon.) Se ni neglektas la sinsekvan (ne samtempan) decidon, la situacio estas analoga al tiu de la prizonula dilemo, sed la ludo estas nun (ofte) ripetebla: El unufoja trompo B povas profiti 9 unuojn, sed el (ekzemple) 20-foja komercado li povas profiti pli. (Tiu principo probable ludas gravan rolon en la ekonomio.)
Interesa demando estas, kiom da fojoj necesas ripeti ludon por certigi, ke ludantoj havas intereson plenumi faritajn interkonsentojn. Se ni konsideras la ripetatan kaŝ-komercon, ni trovas, ke ĝi strukture identas kun la ludo, kiun ni supre nomis "ĉesi ĝustatempe". Kiel ni vidis, la nombro de la paŝoj tie ne gravas; estas ĉiam prudente ĉesi tuj. Same en la ripetata kaŝ-komerco estas prudente neniam kunlabori, alie la partnero povus ekspluati onies fidon en la sekva paŝo.
Iu ajn finia nombro da paŝoj do estas malsufiĉa por doni al la ludantoj raciajn motivojn plenumi siajn promesojn. Nur la ebleco daŭrigi la ludadon sen fiksa limo rompas la argument-ĉenon, kiu devigas al nekunlaboro.
Se ni supozas, ke ludantoj trovis iun vojon por reciproke certigi la plenumon de faritaj interkonsentoj, ekestas la demando, kiun komunan strategion elekti. Estas tre malfacile komvinki alian ludanton pri kunlaboro sen pruvi iun specon de justeco de la interkonsento; kiu sentas sin ege maljuste traktata, emas serĉi ian "ripeton" de la ludo eĉ sur alia kampo, por venĝi sin, kaj eĉ kiel racia aganto ne nepre agas laŭ siajn momentaj interesoj. Konsideru la ludon, en kiu du homoj dividas 100 mon-unuojn: La unua faras proponon pri divido, la dua devas akcepti aŭ rifuzi, kaj ĉe rifuzo ambaŭ ricevas neniom. Laŭ la senripeta teorio la unua devus proponi, ke li ricevu 99 kaj la alia 1, kaj tiu ĉi preferus 1 al 0 kaj akceptus. Sed reale li verŝajne kolerus, rifuzus la 1 mon-unuon por "puni" la alian per perdo de (ni diru) 50. Do, ia justeco necesas; sed kiel difini ĝin?
En ludo absolute simetria oni verŝajne interkonsentas, ke ĉiuj ludantoj havu egalan pagon, aŭ egalajn ŝancojn (ekspektojn), se oni devas uzi miksitajn strategiojn. Sed kiel oni procedu en nesimetriaj situacioj, kiuj ja tre oftas en la vivo? Pri tiu demando interalie okupiĝis la Nobel-premia trio de 1994. Jam plurajn jardekojn antaŭe Nash publikigis sian faman solvon por tiu problemo.
Justeco estas tre abstrakta nocio kaj ne difinebla sen iu sistemo de interkonsentitaj aksiomoj. Por starigi tian sistemon, necesas fari certan simpligon en la analizo de la ludoj, kiu tamen ne esence restriktas la ĝeneralecon.
La dua el tiuj kondicxoj estas tre interesa, ĉar ĝi forte simpligas la analizon de ludo. Sed necesas ne forgesi, ke post tiu simpligo ne plu eblas decidi, ĉu iu ludanto havas intereson kunlabori kaj plenumi interkonsentojn; tion necesas certigi alimaniere, ekzemple per restrikto al pareto-optimumaj punktoj (tiam neniu ludanto havas intereson unuflanke devii) aŭ per eksterludaj fortoj.
Sub la tri kondiĉoj ludo konsistas simple el punktaro en la spaco de la pagoj; tiu punktaro estas konveksa (pro la miksitaj strategioj) kaj kompakta (fermita kaj barata, pro la finieco de la ludo). Solvo de la problemo de justeco konsistas en la trovo de funkcio, kiu asignas al ĉiu tia punktaro unu el ties punktoj kiel la kunlaboran strategiaron.
Kiel ekzemplon ni konsideru variaĵon de la interseksa batalo, en kiu la du paruloj povas marĉandi kaj havas jenan pagomatricon:
| X iras al | |||
|---|---|---|---|
| ekspozicio | koncerto | ||
| Y iras al | ekspozicio | (3;1) | (0;0) |
| koncerto | (0;0) | (1;3) | |
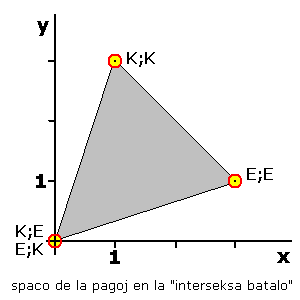
La bildo montras, ke la pagoj de la kvar puraj strategioj okupas tri malsamajn punktojn; laŭ la rezulto estas al la ludantoj egale, ĉu ili enuas solaj en koncerto aŭ ekspozicio. (Tio ne signifas, ke tiu diferenco ne gravas por la ludo, sed ĝi ignoreblas, se estas interkonsento pri kunlaboro.) Per transiro al miksitaj strategioj ekestas la aro de la pago-ekspektoj markita per griza koloro.
Naiva sento pri justeco diras en tiu simetria situacio, ke la ekspekta pago estu egala por la du ludantoj, do la koncerna miksa strategio estu sur la duoniganto de la kvadranto. Kompreneble ĝi estu laŭeble alta, kio tie ĉi ekvivalentas al pareto-optimumeco; do ĝi situu meze de la puraj strategioj (E;E) kaj (K;K) kaj valoru (2;2). Do la ludantoj devus hazarde per egalaj probabloj decidi pri komuna iro al K aŭ E, same kiel la "sana racio" ja tuj dirus.
La du ĵus starigitaj kondiĉoj, simetrieco kaj pareto-optimumeco, ludas gravan rolon en ludo-teoriaj konsideroj pri intertraktado pri justa kunlaboro.
|
|
komenco
|
sekva leciono
|