En la antaŭa leciono ni vidis, ke strategio regata de alia strategio povas resti ekster konsidero. Tio estas grava helpilo por redukti la kompleksecon de ludoj: Oni povas simpligi ludojn per sinsekva eliminado de regataj strategioj. Eblas, ke en tiu procezo aliaj strategioj fariĝas regataj, do necesas ripeti la eliminadon tiom longe, kiom estas ŝanĝo.
Bedaŭrinde regantaj strategioj ne estas vere oftaj. Ŝatata ekzemplo por regantaj strategioj estas la fama prizonula dilemo (aŭ "dilemo de la du prizonuloj").
"La polico arestas du suspektulojn pro grava krimo, kiun minacas puno de 20-jara mallibereco. Tamen ne estas pruviloj, escepte de pafiloj, kies posedon oni punas per unujara mallibereco. La prokuroro faras al ĉiu arestito aparte jenan oferton:
- Se unu konfesas kaj atestas kontraŭ la alia, li liberiĝos, dum ke la alia havos siajn 20 jarojn.
- Se tamen ambaŭ konfesas, ili ricevos po nur kvin jarojn, por rekompenci honestecon kaj penton.
La matrico de la ludo estas jena:
| Prizonula dilemo | |||
|---|---|---|---|
| B | |||
| konfesas | ne konfesas | ||
| A | konfesas | 5;5 | 0;20 |
| ne konfesas | 20;0 | 1;1 | |
La "pagoj" estas la malliberaj jaroj, kaj la ludantoj kompreneble volas minimumigi la proprajn; do se oni volas havi la kutiman maksimumigan situacion, necesas aldoni minusan signon al la pagoj. Oni facile vidas, ke la ludo ne estas konstant-suma: La kvar strategi-kombinoj rezultigas pago-sumojn de 2, 10 kaj 20. Sed ĉar la arestitoj ne rajtas komuniki, la ludo estas konkura.
Same facile oni vidas, ke ĉiu ludanto havas regantan strategion, nome "konfesi", kiu regas la strategion "ne konfesi": depende de la elekto de la "kontraŭulo" la konfeso donas 5 jarojn anstataŭ 20 aŭ 0 jarojn anstataŭ 1, do ambaŭokaze klaran avantaĝon. En tia situacio, se la ludantoj decidas "racie" kaj ne gvidate de iu "krimula honoro" aŭ "principa silento" (itale "omertà"), la rezulto de la ludo estas klara: Ambaŭ konfesas kaj malliberas por 5 jaroj.
Kio okazas, se en dupersona ludo ambaŭ ludantoj havas regantan strategion, kiel en nia ekzemplo? Tiam neniu ludanto havas intereson ludi ion alian ol tiujn strategiojn, kaj la ludo estas determinata. La krucpunkto de la du strategioj havas la econ, ke por ĉiu ludanto ĝi donas la plej altan pagon inter ĉiuj liaj strategioj (por konstanta strategio de la kontraŭulo). En nul-suma ludo tio signifas, ke en la matrico de la pagoj de la linia ludanto (kiu elektas inter la linioj de la matrico) tiu krucpunkto havas maksimuman valoron en la kolumno (aliel la linia ludanto elektus alian linion) kaj minimuman valoron en la linio (aliel la kolumna ludanto elektus alian kolumnon). Alidire tia punkto estas maksimumejo laŭ la influkapablo de unu ludanto kaj minimumejo laŭ tiu de la alia, do ĝi samtempe estas maksimino kaj minimakso. Matematike tia punkto nomiĝas "sela punkto", ĉar la centra punkto de selo havas tiun econ. La koncepto de sela punkto en la strategia spaco originas de von Neumann.
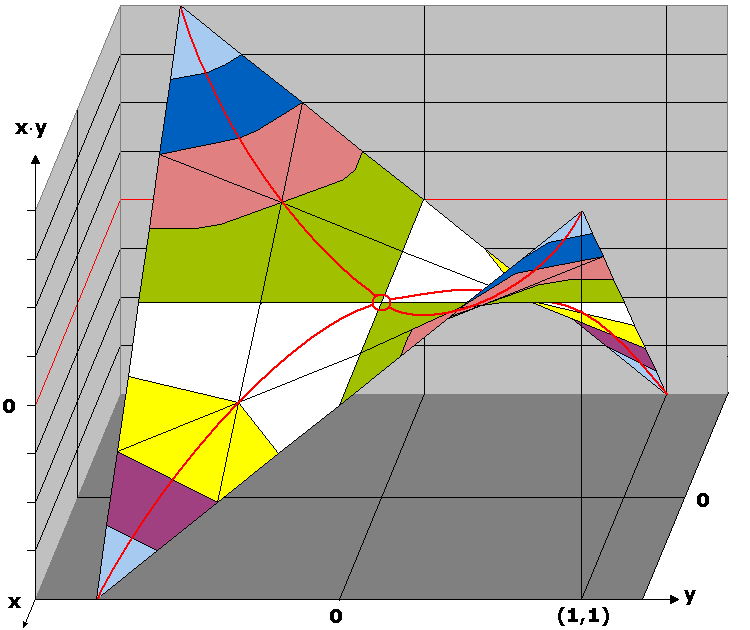
La sel-formon de sela punkto oni bone vidas nur ĉe kontinuaj pago-funkcioj, ekzemple en jena (ne tre interesa) ludo: Du ludantoj samtempe elektas po unu nombron inter (-1) kaj (+1); la unua devas pagi al la dua la produton de la du nombroj. Se ĝi estas negativa, la pago kompreneble estas inversa. La pagofunkcion xy montras jena bildo:

Evidente ĉiu ludanto, kiu elektas "0", plene regas la ludon; la elekto de la kontraŭulo ne plu gravas. La centra punkto, en kiu ambaŭ elektas 0, estas sela punkto.
Tian selan punkton, kiu reprezentas regantan strategion de ambaŭ ludantoj, oni nomas ankaŭ ekvilibro; neniu ludanto havas racian intereson ne elekti la regantan strategion.
Kiam en 1994 la Nobel-premio pri ekonomiko iris al la triopo J. Harsanyi / J. Nash / R. Selten, ĝi estis "pro ilia pionira analizo de ekvilibroj en la teorio de ne-kunlaboraj ludoj", do ĝuste pri la demando, kiel atingi "solvojn" de tiaj ludoj.
Nash (en 1951) proponis jenan ĝeneraligon de la selpunkta koncepto al la kazo de pli ol du ludantoj: strategi-kombino estas ekvilibro ("e. de Nash", "Neŝa e."), se el ĝi neniu ludanto povas per ŝanĝo de sia strategio plibonigi sian pagon.
Alia, ekvivalenta difino de la Neŝa ekvilibro uzas la koncepton de la "optimuma reago". Ludanto povas al donita opo de la strategioj de ĉiuj aliaj lingvoj elekti reagon, kaj tiu(j) strategio(j), kiu(j) donas al li la plej bonan pagon, estas la optimuma reago al la donita strategiaro. Se iu punkto en la ludo havas la econ, ke ĉies strategio estas la optimuma respondo al la opo de la aliaj strategioj, tiam la punkto estas Neŝsa ekvilibro.
Ni analizu kelkajn niajn ekzemplojn pri ekvilibroj:
En ne-kostant-sumaj ludoj povas esti, ke ludantoj havas interesojn ne strikte kontraŭajn, tiel ke certe kunlaboro estas profitiga por ĉiuj. Kaj la prizonuloj kaj la oligopolo montras, ke ekvilibroj neniel garantias ian maksimuman komunan utilon (suman profiton) en tiaj situacioj. Do povas esti ĝene por la ludantoj pensi "ni ambaŭ povus profiti pli". Tio, kompreneble, validas nur por la kazo, ke inter la ludantoj eblas intertraktado kaj interkonsentoj, ke la ludo do ne estas strikte konkura. En tia okazo estas (komune kaj individue) racie, alstrebi maksimuman komunan (suman) pagon.
Por atingi tion oni konsideras nur punktojn, kies pagojn ne eblas "ĉiusence" plibonigi, tiel ke en alia punkto neniu ludanto ricevu malpli kaj almenaŭ unu ludanto pli. Tia punkto nomiĝas "pareto-optimuma" (laŭ Vilfredo Pareto, 1848–1923, itala-franca sciencisto, kiu instruis en Svislando). Denove ni rigardu kelkajn el nia ekzemploj:
|
|
komenco
|
sekva leciono
|