| A | P | S | T | |
|---|---|---|---|---|
| A | 0 | -1 | +1 | +1 |
| P | +1 | 0 | +1 | -1 |
| S | -1 | -1 | 0 | +1 |
| T | -1 | +1 | -1 | 0 |
En niaj ekzemploj pri tabulaj ludoj ĉiuj ludantoj ĉiam havis egalan kaj kompletan informon pri la situacio de la ludo; nekonata estis nur la estonteco. Nun ni konsideru ludojn, en kiuj ne estas tiel.
Estas pluraj manieroj, laŭ kiuj al ludantoj povas manki informo pri la ludo. Ĉe la pli multaj kartoludoj ĉiu ludanto "posedas" kelkajn kartojn, kiujn li kaŝas de la aliaj ludantoj. (Inverse, tre efika trompo ĉe tiaj ludoj estas la markado de la dorsaj kartoflankoj, por igi ilin distingeblaj.)
Alia speco de ludoj uzas ne alternajn, sed samtempajn movojn de la ludantoj, kio implicas, ke informo pri alies movo ne estas havebla por la decido pri la propra. La situacio estas simila al tiu de kaŝitaj informeroj, ĉar antaŭ la movo ĉiu scias sian propran decidon, sed ne tiun de aliaj, same kiel ĉe kaŝitaj kartoj. Diferenco inter la du situacioj estas, ke la propran decidon eblas influi, sed la propran kartaron ne.
La ludoteorio havas malsamajn esprimojn por la du situacioj. Kiam iu informo estas nek konata al nek influebla de iu ludanto, oni parolas pri nekompleta informo. Ekzemplo estas la sinsekvo de nevideblaj kartoj en surtabla (neŭtrala) stako. Se informo estas konata nur al parto de la ludantoj aŭ influata de iu(j) ludanto(j) (per ties decidoj), oni parolas pri neperfekta informo. Ludoj kun samtempaj movoj de pli ol unu ludanto estas ĉiam ludoj kun (almenaŭ) neperfekta informo.
Eblas transformi ludon kun nekompleta informo al ludo kun (nur) neperfekta informo per enkonduko de la naturo kiel ludanto. Tiu naturo ne havas intereson en la rezulto de la ludo, ĝia pago do estas ĉiam nula. Ĝiaj decidoj okazas ne laŭ "racio", sed laŭ donitaj probablecoj.
Se du ludantoj havas samtempa(j)n movo(j)n kaj po finian nombron da strategioj, eblas prezenti la ludon en la formo de matrico, kies flankoj estas indicitaj per la strategioj kaj kies enhavo estas la pagoj por la ludantoj. Ĝenerale estas paroj da pagoj, sed en "nul-suma" ludo, kie la perdo de unu estas la gajno de la alia, sufiĉas doni la pagojn de unu ludanto; tiuj de la alia estas iliaj negativaĵoj.
Ni konsideru ekzemplon kun po du strategioj:
| B1 | B2 | |
|---|---|---|
| A1 | 5 | 1 |
| A2 | 2 | 3 |
Tio signifas, ke se la unua ludanto A ludas A1 kaj la dua B1, la unua ricevas de la dua pagon de 5, ktp.
Se la ludantoj decidus sinsekve, unue A kaj poste B, oni povus analizi la ludon kiel ĉi-supre: B dezirus maksimumigi sian pagon, do minimumigi tion, kion li devas doni al A; li do al A1 reagus per B2 (perdante 1 prefere ol 5) kaj al A2 reagus per B1 (perdante 2 prefere ol 3). Do A decidus favore al A2, per kiu li ricevas 2 prefere ol nur 1.
Se la sinsekvo estus alia, unue B kaj poste A, oni analizus jene: A dezirus maksimumigi sian pagon; li do al B1 reagus per A1 (gajnante 5 prefere ol 2) kaj al B2 reagus per A2 (gajnante 3 prefere ol 2). Do B decidus favore al B2, per kiu li perdas nur 3 prefere ol 5. La sinsekvo de la ludantoj do influas la rezulton.
Sed nun la ludantoj decidu samtempe, tiel ke neniu scias la decidon de la alia. La situacio estas malsama, sed tamen eblas apliki la samajn analizojn kiel en la sinsekva versio: se ĉiu ludanto analizas, kvazaŭ li decidus kiel unua kaj havus racian kontraŭulon, li garantias al si la minimuman pagon, kiun li ricevus en la sinsekva ludo. Laŭ tiu principo A do decidas je A2 kaj B je B2, tiel ke rezultas pago de 3.
Ĉiu ludanto do maksimumigas sian (inter ĉiuj kontraŭulaj strategioj) minimuman pagon. Tiu minimum-maksimumiga strategio nomiĝas ankaŭ maksimin-strategio kaj ĝia pago la maksimino de la ludo. La maksimino de la alia ludanto estas foje nomata minimakso, ĉar pro la inverseco de siaj pagoj li minimumigas inter la maksimumoj de la unua ludanto.
La maksimino de nia ludo estas do 2, la minimakso 3. La du malegalas, kaj el tiu fakto rezultas certa nestabileco de la ludo: B trovus, ke la elektita strategi-kombino (A2, B2) estas por li malpli bona (perdo de 3) ol la najbara (A2, B1) (perdo de 2); do li estas tentata ŝanĝi sian strategion al B1. Tiam A trovus, ke (A2, B1) estas por li malpli bona (gajno de 2) ol la najbara (A1, B1) (gajno de 5), kaj do emus ŝanĝi sian strategion al A1. Poste B trovus, ke (A1, B1) estas por li malpli bona (perdo de 5) ol la najbara (A1, B2) ktp. Tia malstabileco ne aperas, kiam minimakso kaj maksimino estas egalaj. Pri tio ni ankoraŭ parolos.
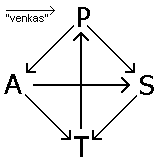
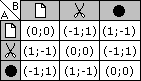
Tiu ludo (mallonge PTŜ), kvankam de tre simpla strukturo, montras multajn interesaĵojn pri ludoj kun samtempaj movoj. Ĝi estas perfekte simetria, do evidente ĉiu ludanto havas egalajn ŝancojn. La sekva diagramo montras la matrican formon de la ludo. La unua bildo montras kiel "rezultojn" la gajnanton, A aŭ B. Pli ĝenerala estas la dua bildo, kiu montras kiel rezultojn la "pagojn" por la du ludantoj; ekzemple, se A ludas "paperon" kaj B "tondilon", la tondilo venkas, B ricevas pagon de "1" kaj A pagon de "-1" (t. e. li devas pagi).

Evidente estus facile venki, se oni scius (divenus) la decidon de la kontraŭulo. Kaj eble ja pli bonajn ŝancojn havas la ludanto, kiu pli bone konas la psikon de la alia kaj kapablas diveni ties strategion. Kontraŭ tio helpas nur unu meta-strategio (strategio pri strategioj): Decidi inter la (tri) eblaj strategioj per hazardo, ekzemple per la ĵeto de kubo. Tio fiaskigas ĉiujn diven-provojn kaj mezume garantias egalajn rezultojn.
Se oni nomas la tri eblajn strategiojn (de unu ludanto) per la literoj P, T, S, la priskribita "miksa" strategio estas
Tiun strategion oni ne povas "venki", t. e. ne ekzistas kontraŭ-strategio, kiu mezume gajnas kontraŭ ĝi. Aliflanke ĝi ankaŭ ne venkas, ĝi mezume ne gajnas pli ofte ol ĝi malgajnas. Ĉar ambaŭ ludantoj povas apliki ĝin, la ludo, se ofte ripetata, fariĝas (teorie) seninteresa; ĝi estas "solvita".
Sen-hazardaj strategioj, kiuj do klare preskribas kion fari, nomiĝas "puraj" strategioj. Miksi plurajn purajn strategiojn per hazardigo estas tre utila tekniko. Multajn ludojn, kiel tiun ĉi, eblas solvi nur per hazardigo.
Ni resumu la renkontitajn terminojn kaj aldonu kelkajn novajn, kiuj faciligos al ni paroli pri ludoj.
La rezulto de ludo estas nomata ties pago. Ĉiu ludanto fine de la ludo ricevas pagon (kiu povas esti negativa, do li devas pagi). Devas esti klare, kiu el du pagoj estas preferata de kiu ludanto; ideale la pago konsistas en io mon-simila, tiel ke ĉiu ludanto preferas havi pli ol malpli.
La eblaj decidoj ("movoj") de la ludantoj nomiĝas strategioj. Miksita strategio estas strategio decidata de hazardo, sed laŭ probablecoj donita de la ludanto. Pura strategio estas strategio sen hazarda elemento (aŭ kie iu decido havas la probablecon 1).
Eblas demandi, kiun sencon havas probablecoj en ludo ludata nur unufoje. Sed miksitaj strategioj estas kutime uzataj tie, kie racia decidmetodo inter pluraj ebloj ne ekzistas. Ili estas la sola metodo por certigi, ke la alia(j) ludanto(j) ne divenu la decidmetodon kaj profitu el tio.
Ludojn similajn al PTŜ oni nomas "matricaj ludoj", ĉar iliaj strategioj kaj pagoj estas bone prezenteblaj en la formo de matrico. Matrica ludo estas ludo inter finia nombro da ludantoj, kiuj havas po finian nombron da strategioj. La dimensio de la pago-matrico estas egala al la nombro de la ludantoj; la longecoj de ĝiaj eĝoj egalas la nombrojn de la strategioj. En la ekzemplo PTŜ estas du ludantoj kun po tri strategioj: do la matrico estas du-dimensia matrico de 3×3 ĉeloj.
Konkuraj ludoj estas ludoj, en kiuj la ludantoj ne kunlaboras. Tion oni plej bone certigas malpermesante komunikadon ekster la lud-scenaro. Konkureco ne signifas, ke ne povas ekzisti parte komunaj interesoj inter la ludantoj, sed nur, ke ili ne povas intertrakti aŭ formi koaliciojn. La ludoteorio okupiĝas ankaŭ pri intertraktado, sed ni unue okupiĝos nur pri konkuraj ludoj. La ekzemplo de la "interseksa batalo" montras, ke malgraŭ komunaj interesoj ludo povas esti komplete konkura.
Kiuj ludoj ne estas matricaj? Unue tiuj kun pli ol finie da ludantoj (ne tre kutima) aŭ nefinie da strategioj (ekzemplo: la du glaciaĵvendistoj). Ekzemplo de ĉi-tio estas ludo, en kiu du ludantoj elektas po naturan nombron; tiu kun la pli alta nombro gajnas.
Ankaŭ ne matricaj estas kompreneble la ludoj kun alternaj movoj (kiel ŝako) kaj la ludoj kun hazardaj elementoj (kartomiksado, kubĵetado). Tamen eblas konsideri la "naturon" (aŭ la fizikon) kiel kroman ludanton kaj atribui al ĝi la rolon decidi pri la hazardaj elementoj.
La strebon de ludanto optimumigi sian gajnon (pagon) nomiĝas ties racia agado. Aliaj streboj, ekzemple plilongigi la ludon pro plezuro aŭ malutili al aliaj ludantoj ("envio"), ne ekzistas en la ludoteorio. Por ilin trakti necesas transformi aŭ enkludi ilin en la pago-sistemon.
Se la naturo aŭ fiziko partoprenas en ludo, ĝi estas la sola ludanto, kiu ne agas racie. Ekzemple oni povas konsideri la decidon, ĉu kunporti pluvombrelon aŭ ne, ludo kontraŭ la naturo; sed la naturo certe ne havas "intereson" malsekigi la ludanton, eĉ se foje tiel ŝajnas. Sekve oni ne atribuas al la naturo pagon.
Ludoj, en kiuj la sumo de la pagoj al ĉiuj ludantoj estas la sama por ĉiuj kombinoj de strategioj, nomiĝas konstant-sumaj ludoj; se la tiu sumo estas ĉiam nula, nul-sumaj ludoj. Tiaj ludoj estas interesaj pro du kialoj:
PTŜ estas ekzemplo por nul-suma ludo, same loterioj (se oni prenas la organizanton inter la ludantojn).
Foje oni ludas variaĵon de la ludo papero-tondilo-ŝtono, aldonante simbolon por "akvoputo". Ĝi estas tre potenca; ŝtono kaj tondilo dronas en ĝi (estas venkataj), nur papero povas ĝin kovri (aŭ flosi sur ĝi). Do ne plu estas simetrio inter la simboloj: Du (A kaj P) venkas po du aliajn, la aliaj du (S kaj T) venkas nur po unu. La matrico de la ludo aspektas jene (ni notas nur la pagojn al la unua, maldekstra, ludanto):
|

|
La ludo ja ankoraŭ estas simetria inter la du ludantoj, sed ne plu inter la strategioj: Oni povus supozi, ke la puraj strategioj A kaj P estas preferindaj al S kaj T. Tamen ĉiu pura strategio restas venkebla, kaj ni povus serĉi hazardigitan optimuman strategion, kiu miksas la kvar purajn strategiojn per la kvar probablecoj a, p, s kaj t. Por kalkuli optimuman ne helpas simpla simetrieca argumento, sed ĉar optimuma strategio ja devas ne malgajni kontraŭ iu ajn strategio, ĝ devas ne malgajni ankaŭ kontraŭ la kvar puraj strategioj (de la kontraŭulo). Tio donas al ni kvar malegalaĵojn, kiuj diras, ke la pago por ludado kontraŭ la kvar puraj strategioj ne estas negativa:
| (1) | (ludo kontraŭ A) | p - s - t ≥ 0 |
|---|---|---|
| (2) | (ludo kontraŭ P) | -a - s + t ≥ 0 |
| (3) | (ludo kontraŭ S) | a + p - t ≥ 0 |
| (4) | (ludo kontraŭ T) | a - p + s ≥ 0 |
Adiciante la malegalaĵojn (1), (2) kaj (4) oni ricevas
(1+2+4) (p - s - t) + (-a - s + t) + (a - p + s) = -s ≥ 0
Ĉar s estas probableco, ĝi estas ne-negativa, ĉi-tie do nula, kio signifas, ke oni neniam uzu S (= ŝtono). Kun tiu rezulto la malegalaĵoj donas jenajn pliajn informojn:
| (1') | p ≥ t |
|---|---|
| (2') | t ≥ a |
| (4') | a ≥ p |
| ⇒ | p ≥ t ≥ a ≥ p |
| ⇒ | p = t = a = 1/3 |
Jen rezulto eble iom surpriza: Sen scio pri la kontraŭula strategio estas optimume ludi egalprobable A, P kaj T kaj neniam S. La ludo per tio kvazaŭ reduktiĝis al la antaŭa ludo kun tri egalpotencaj simboloj. Tamen la kontraŭulo havas la "ŝancon" fari eraron kaj elekti S, kio kaŭzos al li mezuman perdon de 1/3, ĉar ŝtono venkas nur tondilon.
Iom ekster la ludoteorio ni povas demandi nin, kio estas la "enhava" malavantaĝo de la strategio S. Unue, S kaj T venkas nur po unu alian strategion, kio estas malavantaĝo kontraŭ A kaj P; ni do povas nomi ilin "malfortaj" strategioj. Due, T estas la sola kiu venkas P, do estas iel "nemalhavebla", sed S ne estas la sola, kiu venkas T. Alia vido de la ludo montras, el la kvar sub-ludoj, kiuj ekestas per forpreno de unu strategio, nur du estas interesaj, nome {P, A, T} kaj {P, S, T}, kaj la dua estas facile atakebla de la strategio A. Eble la plej simpla klarigo estas, ke la strategio S estas regata de la strategio A: Kiam S gajnas (aŭ egaligas), ankaŭ A gajnus.
Tio montras al ni la gravan koncepton de regantaj (aŭ dominantaj) strategioj: Se iu strategio A estas por ĉiuj kontraŭ-strategioj ne malpreferinda ol alia strategio B (= donas ne malpli altan pagon ol B) kaj por almenaŭ unu kontraŭ-strategio estas eĉ preferinda (= donas pli altan pagon, oni diras, ke A regas B. Regatajn strategiojn oni povas elimini el la konsiderado, ĉar ili ne alportas utilon.
Pli fajna distingo diras, ke laŭ la supra difini A malforte regas B. Se A donas por ĉiuj kontraŭ-strategioj pli altan pagon ol B, oni diras, ke B estas eĉ strikte regata de A.
Regantaj kaj regataj strategioj estas la plej simpla decidhelpilo en konkuraj ludoj. Ni konsideros kaj traktos ankoraŭ aliajn.
|
|
komenco
|
sekva leciono
|